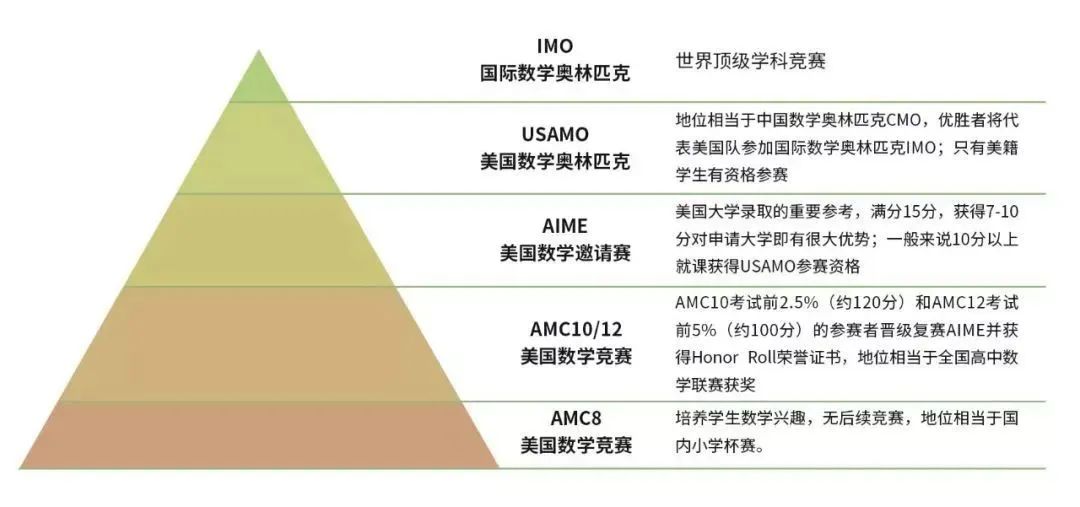
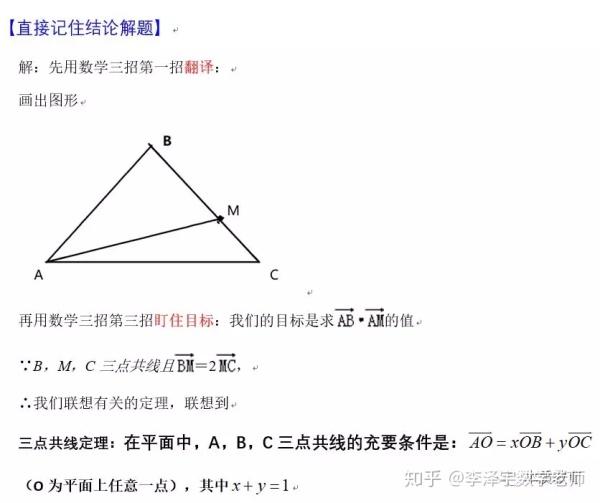
利用平面向量中三点共线定理快速解题
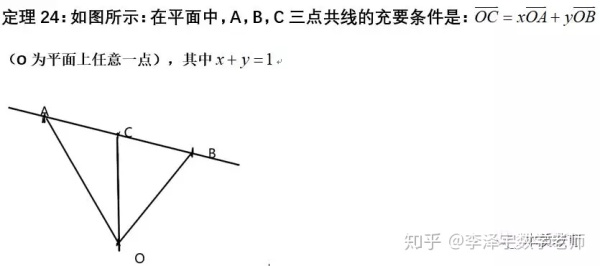


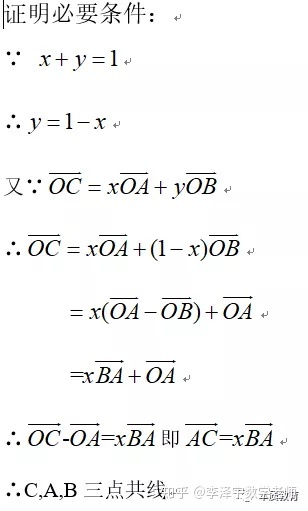



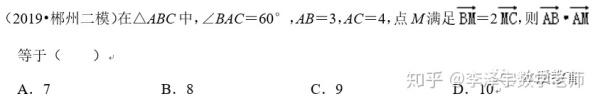


作者:李泽宇数学老师
来源:知乎 


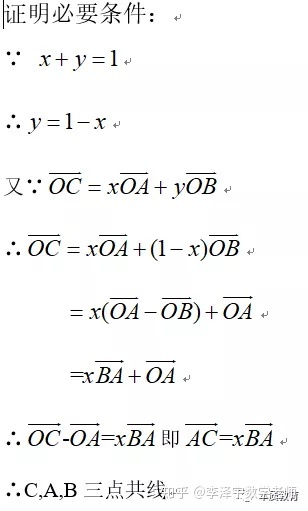



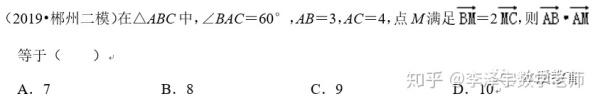



本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。