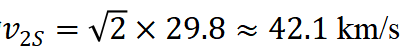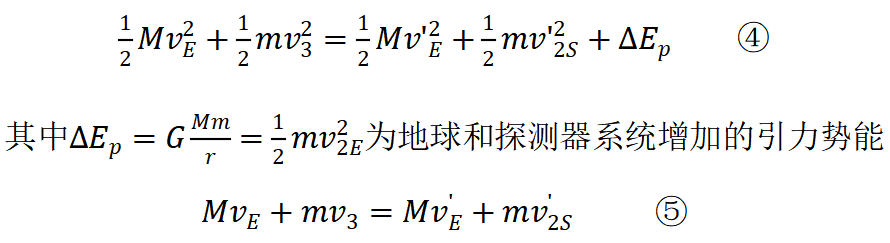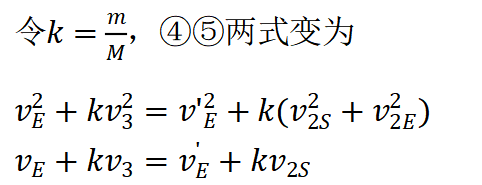以中心天体是地球为例,第一宇宙速度是指“地球表面附近的环绕速度,约为7.9 km/s(粗略取8 km/s)”,第二宇宙速度是指“在地球表面附近脱离地球引力的发射速度,大小是第一宇宙速度的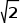 倍,约为11.2 km/s”,第三宇宙速度是指“在地球公转轨道上离开太阳系的速度,约为16.7 km/s(发射时要利用地球公转的30 km/s速度)”。
倍,约为11.2 km/s”,第三宇宙速度是指“在地球公转轨道上离开太阳系的速度,约为16.7 km/s(发射时要利用地球公转的30 km/s速度)”。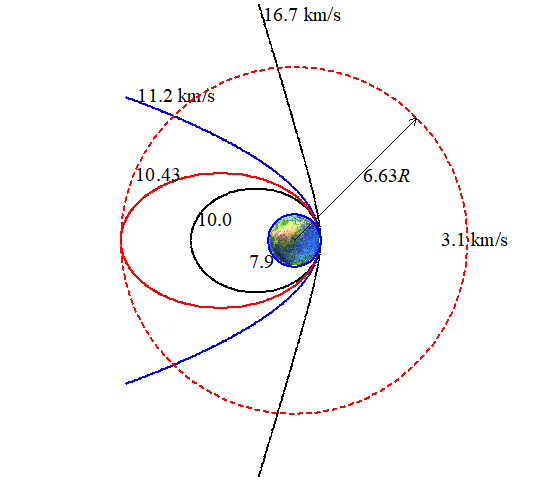 如图所示,地球的三个宇宙速度分别对应三条运动轨迹(7.9 km/s、11.2 km/s、16.7 km/s)。当发射速度超过7.9 km/s时,卫星的轨道变成椭圆,如图中10.0 km/s和10.43 km/s两个轨道,发射速度越大,椭圆的半长轴越长、公转周期越长。当发射速度达到11.2 km/s,探测器(不能再叫做“卫星”了)的轨道变成抛物线,如我国的天问一号火星探测器,长征五号火箭分离时速度已达11.2 km/s。当发射速度达到16.7 km/s时,探测器的轨道变成双曲线,探测器会离开太阳的引力范围。为了区分发射速度和环绕速度,图中绘制了同步卫星的轨道(3.1 km/s)。根据万有引力提供向心力,容易得出轨道越高,卫星的环绕速度越小。
如图所示,地球的三个宇宙速度分别对应三条运动轨迹(7.9 km/s、11.2 km/s、16.7 km/s)。当发射速度超过7.9 km/s时,卫星的轨道变成椭圆,如图中10.0 km/s和10.43 km/s两个轨道,发射速度越大,椭圆的半长轴越长、公转周期越长。当发射速度达到11.2 km/s,探测器(不能再叫做“卫星”了)的轨道变成抛物线,如我国的天问一号火星探测器,长征五号火箭分离时速度已达11.2 km/s。当发射速度达到16.7 km/s时,探测器的轨道变成双曲线,探测器会离开太阳的引力范围。为了区分发射速度和环绕速度,图中绘制了同步卫星的轨道(3.1 km/s)。根据万有引力提供向心力,容易得出轨道越高,卫星的环绕速度越小。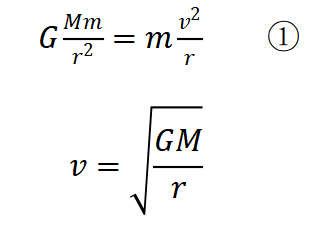 如地球表面附近的卫星速度为7.9 km/s,同步轨道(距地球表面36000 km的高空)上的卫星速度为3.1 km/s。实际上,地球所有卫星的环绕速度都小于7.9 km/s。但是发射一颗地球同步卫星,需要的速度是10.43 km/s(不是3.1 km/s)。一种发射方案是轨道先从“小圆”变成椭圆,再由椭圆变成“大圆”。需要两次变轨,第一次椭圆相对于“小圆”是离心运动,需要加速变轨;第二次椭圆相对于“大圆”是近心运动,需要再次加速变轨。经历两次加速变轨,为什么速度还小于7.9 km/s?那是因为在椭圆轨道上卫星经历了漫长的减速过程(“万有引力做负功,动能减小”或用机械能守恒定律理解“卫星离得越远,引力势能越大,动能越小”),速度由10.43 km/s减为1.57 km/s,远地点速度小于环绕速度(3.1 km/s)。可见,7.9 km/s是所有环绕速度的最大速度,又是所有发射速度的最小速度。
如地球表面附近的卫星速度为7.9 km/s,同步轨道(距地球表面36000 km的高空)上的卫星速度为3.1 km/s。实际上,地球所有卫星的环绕速度都小于7.9 km/s。但是发射一颗地球同步卫星,需要的速度是10.43 km/s(不是3.1 km/s)。一种发射方案是轨道先从“小圆”变成椭圆,再由椭圆变成“大圆”。需要两次变轨,第一次椭圆相对于“小圆”是离心运动,需要加速变轨;第二次椭圆相对于“大圆”是近心运动,需要再次加速变轨。经历两次加速变轨,为什么速度还小于7.9 km/s?那是因为在椭圆轨道上卫星经历了漫长的减速过程(“万有引力做负功,动能减小”或用机械能守恒定律理解“卫星离得越远,引力势能越大,动能越小”),速度由10.43 km/s减为1.57 km/s,远地点速度小于环绕速度(3.1 km/s)。可见,7.9 km/s是所有环绕速度的最大速度,又是所有发射速度的最小速度。
根据势能关系,引力势能的变化量与引力做功互为相反数。引力做正功,引力势能减小(卫星靠近地球时);引力做负功,引力势能增加(卫星远离地球时)。万有引力随着距离发生变化,不是恒力,不能直接计算功。以下利用高中简单的微积分知识,做简要探究。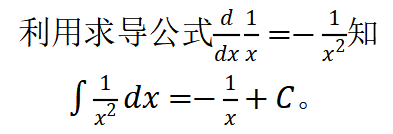 一般取无穷远处的引力势能为零,卫星从无穷远往回走,引力总是做正功,引力势能减小,因此引力势能总是负值。
一般取无穷远处的引力势能为零,卫星从无穷远往回走,引力总是做正功,引力势能减小,因此引力势能总是负值。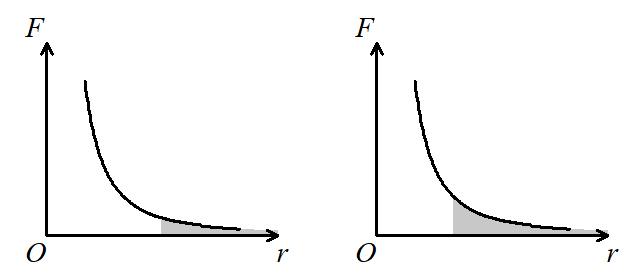 引力做的功为上图右侧的阴影面积,r越小(离得越近),功越大(面积越大)。引力做的功只在半径方向有效(垂直于半径方向引力不做功),当卫星往回走时,位移的方向与半径的方向刚好相反,此时
引力做的功为上图右侧的阴影面积,r越小(离得越近),功越大(面积越大)。引力做的功只在半径方向有效(垂直于半径方向引力不做功),当卫星往回走时,位移的方向与半径的方向刚好相反,此时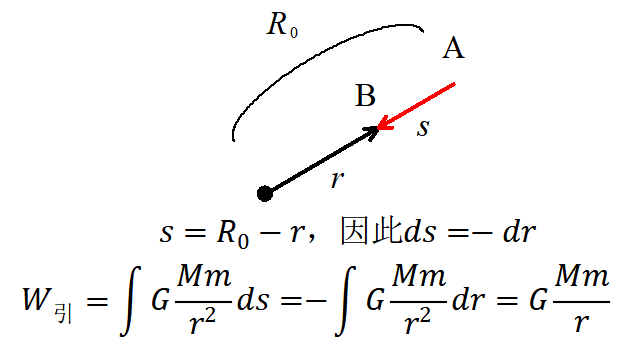
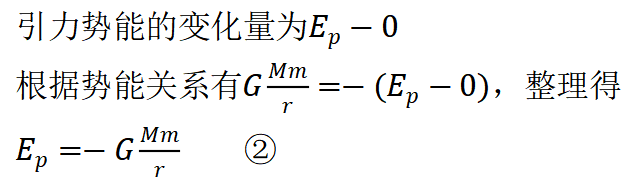 设地球的第二宇宙速度为
设地球的第二宇宙速度为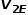 ,以这个速度卫星可以脱离地球引力范围(到达无穷远),此时卫星的动能为零、引力势能也为零。地球和卫星组成的系统机械能守恒
,以这个速度卫星可以脱离地球引力范围(到达无穷远),此时卫星的动能为零、引力势能也为零。地球和卫星组成的系统机械能守恒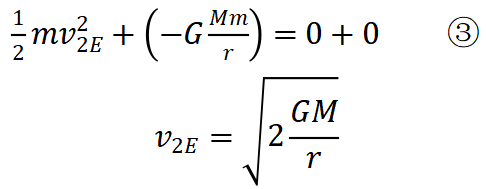 这个速度刚好是环绕速度的
这个速度刚好是环绕速度的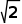 倍,即
倍,即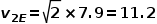 km/s。
km/s。
以太阳为参考系,探测器先要沿地球公转方向离开地球引力范围,此时的动能在地球公转轨道恰好能够离开太阳的引力范围。在轨道上离开引力范围需要的速度刚好是环绕速度的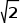 倍。已知地球的公转速度为
倍。已知地球的公转速度为 29.8 km/s,则在地球公转轨道上离开太阳引力需要的速度为
29.8 km/s,则在地球公转轨道上离开太阳引力需要的速度为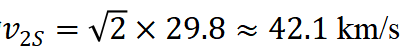 探测器离开地球引力的过程中,可以认为探测器做直线运动,太阳引力对探测器不做功,探测器和地球组成的系统机械能守恒;而且在探测器运动方向上,该系统动量守恒。设探测器离开地球时的速度为v3(第三宇宙速度),因此
探测器离开地球引力的过程中,可以认为探测器做直线运动,太阳引力对探测器不做功,探测器和地球组成的系统机械能守恒;而且在探测器运动方向上,该系统动量守恒。设探测器离开地球时的速度为v3(第三宇宙速度),因此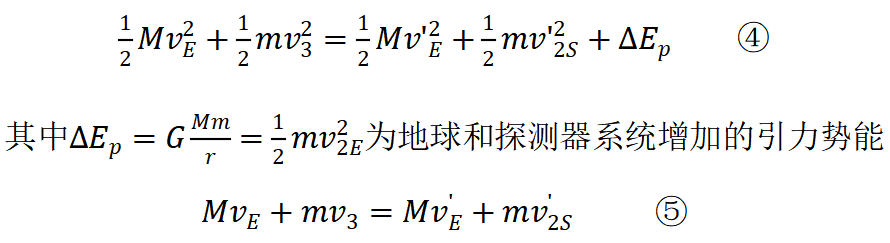
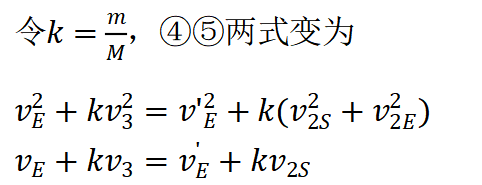

3. 微课要点:本节介绍地球的三个宇宙速度,采用具体数据澄清环绕速度和发射速度,利用微积分初步知识引入引力势能的表达式,应用机械能守恒和动量守恒的概念导出了第二和第三宇宙速度。 本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。
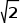 倍,约为11.2 km/s”,第三宇宙速度是指“在地球公转轨道上离开太阳系的速度,约为16.7 km/s(发射时要利用地球公转的30 km/s速度)”。
倍,约为11.2 km/s”,第三宇宙速度是指“在地球公转轨道上离开太阳系的速度,约为16.7 km/s(发射时要利用地球公转的30 km/s速度)”。
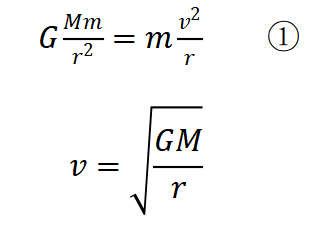
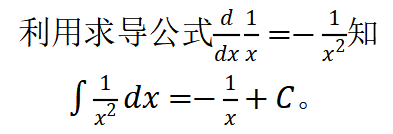

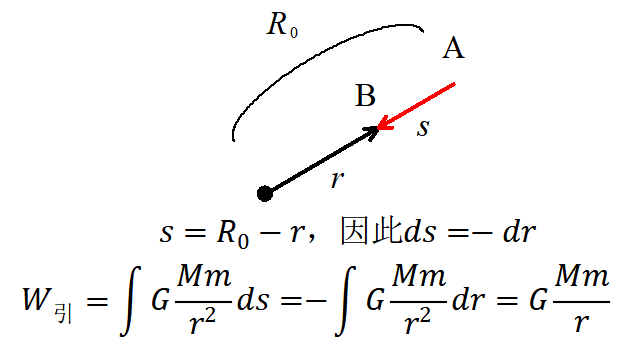
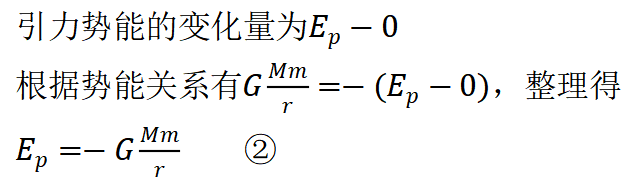
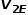 ,以这个速度卫星可以脱离地球引力范围(到达无穷远),此时卫星的动能为零、引力势能也为零。地球和卫星组成的系统机械能守恒
,以这个速度卫星可以脱离地球引力范围(到达无穷远),此时卫星的动能为零、引力势能也为零。地球和卫星组成的系统机械能守恒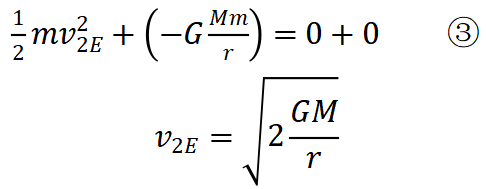
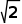 倍,即
倍,即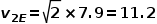 km/s。
km/s。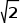 倍。已知地球的公转速度为
倍。已知地球的公转速度为 29.8 km/s,则在地球公转轨道上离开太阳引力需要的速度为
29.8 km/s,则在地球公转轨道上离开太阳引力需要的速度为