
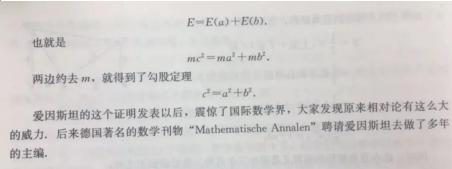 教材中写道:【2005年是爱因斯坦建立相对论 100 周年,爱因斯坦在相对论中给出了一个著名的质能方程 E=mc²,其中 E 表示物质所含的所有能量,m 是物质的质量,c 是光速,这个质能方程是现代制造核武器、核电站的理论基础。】
接着话锋一转,向我们展示了爱因斯坦是如何用相对论“证明”勾股定理的。
首先,假设某一直角三角形的三条边为 a、b、c,同时设这一直角三角形的面积为 E,根据相对论质能方程可知:E=mc²。然后,从直角顶点出发作斜边 c 的垂线段。此时,这一直角三角形被分割成为了两个小三角形,它们的面积分别为:E(a)=ma², E(b)=mb²。
鉴于 E=E(a)+E(b),即 mc²=ma²+mb²。只需要约去式子两边相同的 m,可得 c²=a²+b²。
乍一看,似乎有点道理。也就是说,这里真的成功地用相对论质能方程证明了勾股定理,不禁让人感叹相对论的伟大,真是包罗万象无所不通。
然而从专业的角度来看,其中的“设这一直角三角形的面积为 E,根据相对论质能方程可知:E=mc²”的三角形面积计算方法,完全是用字母替代概念的填字游戏,没有任何物理上的实际意义。
后来,经过大家的查找和分析,最终扒出了关于爱因斯坦这部分证明的段落出处。
教材中写道:【2005年是爱因斯坦建立相对论 100 周年,爱因斯坦在相对论中给出了一个著名的质能方程 E=mc²,其中 E 表示物质所含的所有能量,m 是物质的质量,c 是光速,这个质能方程是现代制造核武器、核电站的理论基础。】
接着话锋一转,向我们展示了爱因斯坦是如何用相对论“证明”勾股定理的。
首先,假设某一直角三角形的三条边为 a、b、c,同时设这一直角三角形的面积为 E,根据相对论质能方程可知:E=mc²。然后,从直角顶点出发作斜边 c 的垂线段。此时,这一直角三角形被分割成为了两个小三角形,它们的面积分别为:E(a)=ma², E(b)=mb²。
鉴于 E=E(a)+E(b),即 mc²=ma²+mb²。只需要约去式子两边相同的 m,可得 c²=a²+b²。
乍一看,似乎有点道理。也就是说,这里真的成功地用相对论质能方程证明了勾股定理,不禁让人感叹相对论的伟大,真是包罗万象无所不通。
然而从专业的角度来看,其中的“设这一直角三角形的面积为 E,根据相对论质能方程可知:E=mc²”的三角形面积计算方法,完全是用字母替代概念的填字游戏,没有任何物理上的实际意义。
后来,经过大家的查找和分析,最终扒出了关于爱因斯坦这部分证明的段落出处。
 事实上,爱因斯坦只是利用了相似三角形的关系,得到了相似三角形的面积比和变长平方的关系,而其中的m是一个非零比例系数,并不是质能方程中的质量m,而其中的E只是对于面积的代指,与质能方程中的E能量毫无关系。
虽然是自读教材,但是在人教版教材上出现这种民科级别的问题也确实令人震惊,近年来,对于国内教材质量的质疑也屡见不鲜,究其原因,体制内教学在数理化等学科上的知识体系不系统与僵化,是造成这种现象的主要原因。随着国际课程在国内的普及,IB、AP、A-level等国际课程都为大家打开了新世界的大门。
事实上,爱因斯坦只是利用了相似三角形的关系,得到了相似三角形的面积比和变长平方的关系,而其中的m是一个非零比例系数,并不是质能方程中的质量m,而其中的E只是对于面积的代指,与质能方程中的E能量毫无关系。
虽然是自读教材,但是在人教版教材上出现这种民科级别的问题也确实令人震惊,近年来,对于国内教材质量的质疑也屡见不鲜,究其原因,体制内教学在数理化等学科上的知识体系不系统与僵化,是造成这种现象的主要原因。随着国际课程在国内的普及,IB、AP、A-level等国际课程都为大家打开了新世界的大门。 本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。

 《爱因斯坦文集》:我的世界观
《爱因斯坦文集》:我的世界观 《爱因斯坦文集》:论教育
《爱因斯坦文集》:论教育 爱因斯坦:数学学习的意义不在于学习一堆知识,而在于思维!
爱因斯坦:数学学习的意义不在于学习一堆知识,而在于思维! 量子纠缠速度起码是光速的10000倍,违反爱因斯坦的相对论吗?
量子纠缠速度起码是光速的10000倍,违反爱因斯坦的相对论吗? 霍金:我眼中的爱因斯坦与相对论
霍金:我眼中的爱因斯坦与相对论 麦克斯韦方程组是否满足相对性原理?爱因斯坦狭义相对论是如何创立的?
麦克斯韦方程组是否满足相对性原理?爱因斯坦狭义相对论是如何创立的? 洛伦兹对称性和相对论有什么关系?验证爱因斯坦时空对称正确性
洛伦兹对称性和相对论有什么关系?验证爱因斯坦时空对称正确性






