看一道自带霸王色霸气的三角函数极限难题：
例： 求极限![[公式]](https://www.zhihu.com/equation?tex=I%3D%5Clim_%7Bx%20%5Crightarrow%200%7D%7B%5Cfrac%7Bcos%28sinx%29-cos%28sintanx%29%7D%7Bx%5E%7B4%7D%7D%7D)
乍一看，你想到了什么方法？没猜错，你应该想到了泰勒展开或洛必达，但如果Kaysen/煜神（148上将）告诉你这道题还能用拉氏中值、和差化积公式玩出花儿来，你有没有兴趣？
（P.S. 注意洛必达此处失效，分子求导当场狗带）
我们先来看看解这道题最基础的泰勒大法：
方法一：泰勒(easy doing，技术创新性★★)
泰勒最麻烦的点就在于能否保证展开的全面性！
方法二：和差化积 拉氏中值 (魔鬼细节，技术创新性★★★★★)
学长看到 ![[公式]](https://www.zhihu.com/equation?tex=cos%5Ctheta_%7B1%7D-cos%5Ctheta_%7B2%7D)
,和差化积啪的一下就蹦出来了，很快啊！
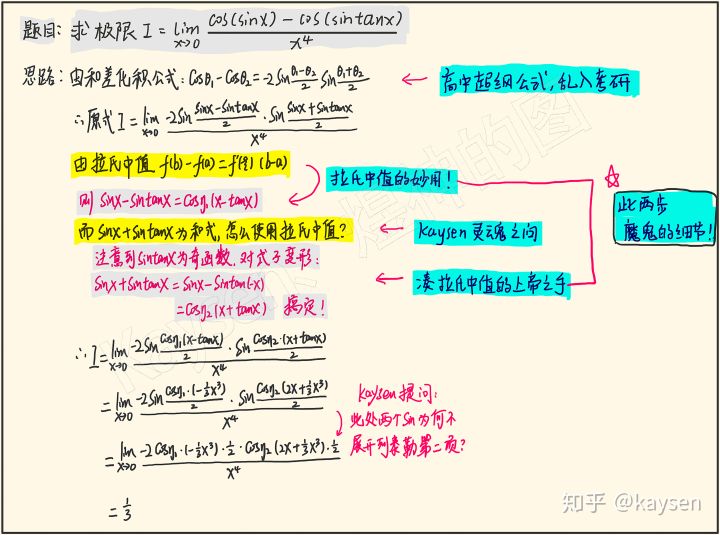和差化积与拉氏中值擦出的绚丽火花
方法三：拉氏中值一般式（技术创新性★★★）
拉式中值 放缩，巧解复杂极限
方法四：拉氏中值有限增量式（技术创新性★★★★★）
当题干某部分函数明显能用拉氏中值，但用一般式又看不出什么名堂（精度不够），又懒得用放缩去讨论，不妨跟学长一起试试有限增量式，看看会发生出什么特异的化学反应！
所谓有限增量式，见同济高数书P128页，有如下一段话，不知大家有无品出余韵：
很多看过同济7版的同学，有限增量定理有没有激发创造性的解题思路？
有限增量，提高参数精度，出奇制胜！ 本站内容收集整理于网络，多标有原文出处，本站仅提供信息存储空间服务。如若转载，请注明出处。
