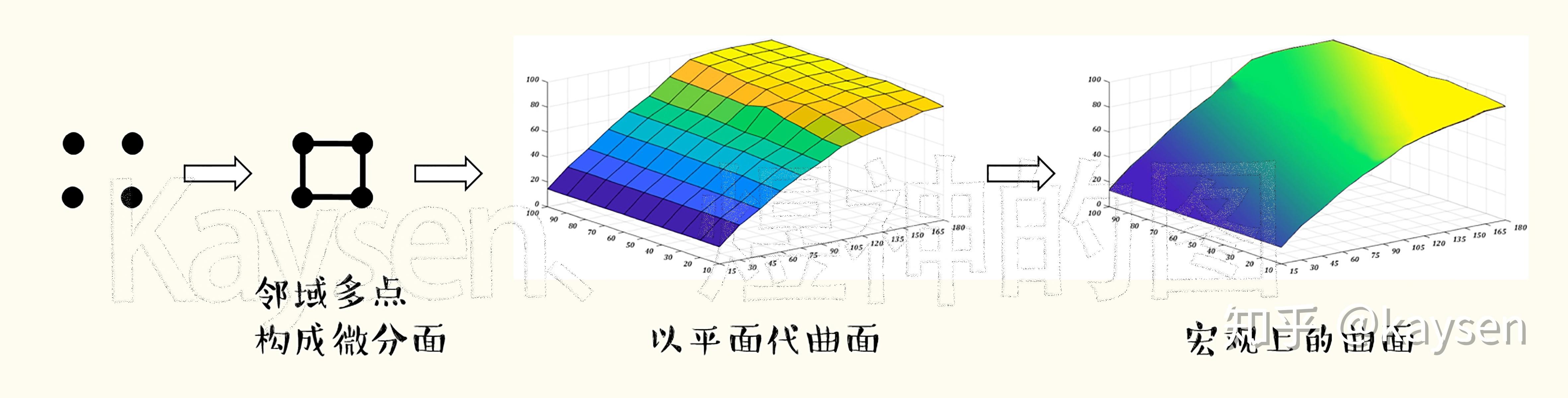
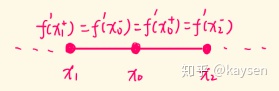二元微分中,连续、可微、可偏导、偏导连续,概念间的辩证关系抽象又难懂,那如何通俗又深刻的搞定它们呢?
先来看看关系网络全地图:
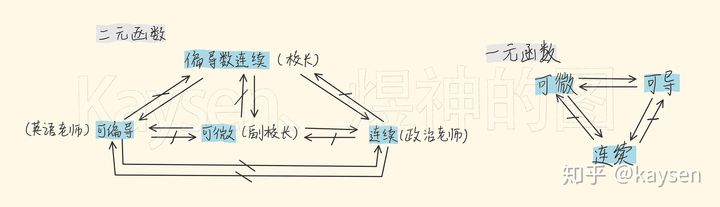 联想一下,疏通筋骨!(注:偏导连续默认指一阶偏导连续)
联想一下,疏通筋骨!(注:偏导连续默认指一阶偏导连续)
一、连续、可微
连续,就是离散的对立统一面。
一元函数中,用直线串联相邻微分点,就构成了宏观连续的平面曲线。
 二元函数中,用微面连接相邻区域,就构成了宏观连续的空间曲面。
二元函数中,用微面连接相邻区域,就构成了宏观连续的空间曲面。
![]() 类似于学长在研究课题中的面网格剖分工作:
类似于学长在研究课题中的面网格剖分工作:
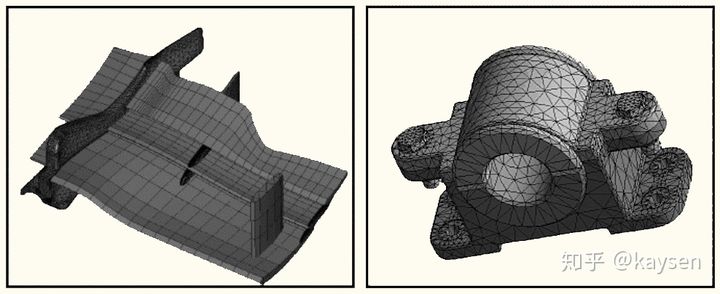 有限元模拟,使用三角形和四边形网格表达零件曲面
有限元模拟,使用三角形和四边形网格表达零件曲面
二、可(偏)导与可微
2.1 一元可导与可微
一元可导,内在地蕴涵着确定性与确定量的要求。
☛比如面试顶尖企业。首先,需要具备确定性。思想坚定不摇摆。
 曲线在
曲线在 ![[公式]](https://www.zhihu.com/equation?tex=x_%7B0%7D) 可导。需要原函数在左右邻域连续,且左导=右导。
可导。需要原函数在左右邻域连续,且左导=右导。
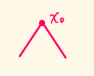 反之这样左右摇摆的尖点,思想不坚定,不符合企业要求。
此处,Kaysen提出一个有意思的悖论,大家可以思考一下。
悖论1:☠
既然
反之这样左右摇摆的尖点,思想不坚定,不符合企业要求。
此处,Kaysen提出一个有意思的悖论,大家可以思考一下。
悖论1:☠
既然 ![[公式]](https://www.zhihu.com/equation?tex=x_%7B0%7D) 可导。要求
可导。要求 ![[公式]](https://www.zhihu.com/equation?tex=f%27%28x_%7B0%7D%5E%7B-%7D%29%3Df%27%28x_%7B0%7D%5E%7B%2B%7D%29%3DA) ,而其左邻点
,而其左邻点 ![[公式]](https://www.zhihu.com/equation?tex=x_%7B1%7D) 的右导
的右导 ![[公式]](https://www.zhihu.com/equation?tex=f%27%28x_%7B1%7D%5E%7B%2B%7D%29%3Df%27%28x_%7B0%7D%5E%7B-%7D%29%3DA) ,右邻点
,右邻点 ![[公式]](https://www.zhihu.com/equation?tex=x_%7B2%7D) 的左导
的左导 ![[公式]](https://www.zhihu.com/equation?tex=f%27%28x_%7B2%7D%5E%7B-%7D%29%3Df%27%28x_%7B0%7D%5E%7B%2B%7D%29%3DA) 。以此类推,整条曲线所有点的导数值均等于A。这样的话,所有曲线不都变成了直线么?
。以此类推,整条曲线所有点的导数值均等于A。这样的话,所有曲线不都变成了直线么?
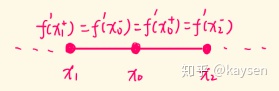 萌萌分割线(思考几分钟后再看学长给出的解释)☺
学长释疑:✍
此为极限思想制造出的悖论。该情境下,局部近似与趋近不能作用于整体。这是由于微观以直代曲的直线斜率,
萌萌分割线(思考几分钟后再看学长给出的解释)☺
学长释疑:✍
此为极限思想制造出的悖论。该情境下,局部近似与趋近不能作用于整体。这是由于微观以直代曲的直线斜率, ![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7B%5CDelta%20x%20%5Crightarrow%200%7D%7B%5Cfrac%7Bf%28x_%7B0%7D%5Cpm%20%5CDelta%20x%29-f%28x_%7B0%7D%29%7D%7B%5Cpm%5CDelta%20x%7D%7D) ,本质是个近似值!
有同学会问,极限仅是
,本质是个近似值!
有同学会问,极限仅是 ![[公式]](https://www.zhihu.com/equation?tex=%5CDelta%20x%20%5Crightarrow0) ,计算出的斜率仍然是个实际值啊!为何学长说是近似值?这位同学且慢!(尔康表情包就不放了)。注意
,计算出的斜率仍然是个实际值啊!为何学长说是近似值?这位同学且慢!(尔康表情包就不放了)。注意 ![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7B%5CDelta%20x%20%5Crightarrow%200%7D%7B%5Cfrac%7Bf%28x_%7B0%7D%5Cpm%20%5CDelta%20x%29-f%28x_%7B0%7D%29%7D%7B%5Cpm%5CDelta%20x%7D%7D) 中,分子与分母为
中,分子与分母为 ![[公式]](https://www.zhihu.com/equation?tex=%E2%80%9C%5Cfrac%7B0%7D%7B0%7D%E2%80%9D) 型,也即是
型,也即是 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%E6%97%A0%E7%A9%B7%E5%B0%8F%7D%7B%E6%97%A0%E7%A9%B7%E5%B0%8F%7D) 型。无穷小量,我们并不能精确把握。它是结果量还是状态量,是定量还是变量?不清不楚。所以当涉及无穷小量计算时。计算出的斜率均为近似值,而非实际值!
型。无穷小量,我们并不能精确把握。它是结果量还是状态量,是定量还是变量?不清不楚。所以当涉及无穷小量计算时。计算出的斜率均为近似值,而非实际值!
无穷个微小偏差。会表现出线条宏观上的巨大改变。正如0.99999的无穷次方。最终也会趋近于0。
☛其次,面试顶尖企业。简历还得具备确定量性。比如在校绩点排名等。增加可信度。
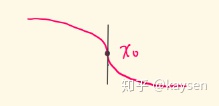 如上图,
如上图,![[公式]](https://www.zhihu.com/equation?tex=x_%7B0%7D) 处斜率
处斜率 ![[公式]](https://www.zhihu.com/equation?tex=%5Crightarrow%20%5Cinfty) ,导数是不存在的,因为无穷并不是一个确定的量。
此处请思考悖论2:☠
既然可微可理解为“以直代曲”,那么在“导数”
,导数是不存在的,因为无穷并不是一个确定的量。
此处请思考悖论2:☠
既然可微可理解为“以直代曲”,那么在“导数” ![[公式]](https://www.zhihu.com/equation?tex=%5Crightarrow%20%5Cinfty) 的点,也有一段直线可以表达曲线,那该点岂不是可微的么?
学长释疑:✍
可微,是人为规定的,通过计算来判断微分各变量之间的精确定量关系,
的点,也有一段直线可以表达曲线,那该点岂不是可微的么?
学长释疑:✍
可微,是人为规定的,通过计算来判断微分各变量之间的精确定量关系,![[公式]](https://www.zhihu.com/equation?tex=dy%3Df%27%28x_%7B0%7D%29dx) ,若
,若 ![[公式]](https://www.zhihu.com/equation?tex=f%27%28x_%7B0%7D%29%5Crightarrow%20%5Cinfty) ,
, ![[公式]](https://www.zhihu.com/equation?tex=dy) 与
与 ![[公式]](https://www.zhihu.com/equation?tex=dx) 的定量关系无法在数值上精确判断,故不可微。若将该图像转角
的定量关系无法在数值上精确判断,故不可微。若将该图像转角 ![[公式]](https://www.zhihu.com/equation?tex=90%20%5E%7B%200%20%7D) ,则
,则 ![[公式]](https://www.zhihu.com/equation?tex=f%27%28x_%7B0%7D%29%3D%200) ,则可微。
,则可微。
总结:一元函数的可导与可微等价,可通俗的认为二者均表示曲线连续且光滑,且切线无竖直情况。
2.2 二元可偏导与可微
![[公式]](https://www.zhihu.com/equation?tex=%E5%8F%AF%E5%BE%AE%5CRightarrow%E5%8F%AF%E5%81%8F%E5%AF%BC%EF%BC%8C%E5%8F%AF%E5%81%8F%E5%AF%BC%E4%B8%8D%E8%83%BD%E6%8E%A8%E5%87%BA%E5%8F%AF%E5%BE%AE) 学长灵魂之问:一元函数可导与可微等价,二元函数咋就不行了呢?
这是因为,一元函数的可导和可微均为一元属性。而二元函数可偏导是一元属性,而可微却是二元属性。一元属性的偏导存在无法推出二元属性的可微。
我们先看看,可微是在说什么?
二元函数在某点可微,表示的是该点处的曲面,可由一个不垂直于
学长灵魂之问:一元函数可导与可微等价,二元函数咋就不行了呢?
这是因为,一元函数的可导和可微均为一元属性。而二元函数可偏导是一元属性,而可微却是二元属性。一元属性的偏导存在无法推出二元属性的可微。
我们先看看,可微是在说什么?
二元函数在某点可微,表示的是该点处的曲面,可由一个不垂直于 ![[公式]](https://www.zhihu.com/equation?tex=xoy) 面的微小切平面代表。
面的微小切平面代表。
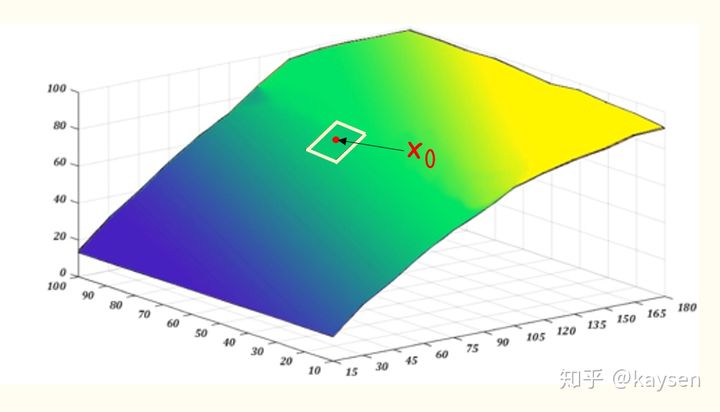 方块虽小,但意义重大
我们将该切平面放大,再放大!来看看这个切平面是怎么得来的,是如何以平面代曲面的。
方块虽小,但意义重大
我们将该切平面放大,再放大!来看看这个切平面是怎么得来的,是如何以平面代曲面的。
 微分平面:我是谁?我从哪儿来?
一元中,可微曲线的以直代曲,是小段切线代替局部曲线。而切线的构成,则是将
微分平面:我是谁?我从哪儿来?
一元中,可微曲线的以直代曲,是小段切线代替局部曲线。而切线的构成,则是将 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bdy%7D%7Bdx%7D%3Df%27%28x_%7B0%7D%29) 中的
中的 ![[公式]](https://www.zhihu.com/equation?tex=dy%20) ,
, ![[公式]](https://www.zhihu.com/equation?tex=dx) 放大成
放大成 ![[公式]](https://www.zhihu.com/equation?tex=y-y_%7B0%7D) 和
和 ![[公式]](https://www.zhihu.com/equation?tex=x-x_%7B0%7D) ,变成
,变成 ![[公式]](https://www.zhihu.com/equation?tex=y-y_%7B0%7D%3Df%27%28x_%7B0%7D%29%28x-x_%7B0%7D%29) 二元中,可微曲面的以平面代曲面,是小面积的切平面代替局部曲面。切平面,又可以看做是该点切线在该平面内旋转一周得到(即线动成面)。这些各向切线的斜率就是该点处的无数个方向导数。如下图。
二元中,可微曲面的以平面代曲面,是小面积的切平面代替局部曲面。切平面,又可以看做是该点切线在该平面内旋转一周得到(即线动成面)。这些各向切线的斜率就是该点处的无数个方向导数。如下图。
 一根切线,转成一个微小的切平面
若切平面不垂直于
一根切线,转成一个微小的切平面
若切平面不垂直于 ![[公式]](https://www.zhihu.com/equation?tex=xoy) 面,可认为该点处可微。(切面垂直于
面,可认为该点处可微。(切面垂直于![[公式]](https://www.zhihu.com/equation?tex=xoy) 面时,导数不存在,类似于一元的理解)
那可偏导又在说什么?
说的是曲面上一点处,平行于
面时,导数不存在,类似于一元的理解)
那可偏导又在说什么?
说的是曲面上一点处,平行于 ![[公式]](https://www.zhihu.com/equation?tex=x) 轴、
轴、 ![[公式]](https://www.zhihu.com/equation?tex=y) 轴的两个方向导数存在。
对于可偏导-可微的辩证关系,可如下理解:"两个线属性存在,并不能推出一个可微的面属性!"——煜神语录。
因为面属性的可微要求从各个方向趋近,而偏导只有两个方向。若用
轴的两个方向导数存在。
对于可偏导-可微的辩证关系,可如下理解:"两个线属性存在,并不能推出一个可微的面属性!"——煜神语录。
因为面属性的可微要求从各个方向趋近,而偏导只有两个方向。若用 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B2%7D%7B%5Cinfty%7D) 代替
代替 ![[公式]](https://www.zhihu.com/equation?tex=%5Cinfty) ,那这就,草率了啊!
按这个思路,举个图形反例,见下:
,那这就,草率了啊!
按这个思路,举个图形反例,见下:
 《生化危机》中保护伞公司的logo示意图
图中雨伞取1,2,3,4面合并为某一曲面,伞柄为Z轴向,假定两条黄虚线为x/y轴向。显然,伞尖处可偏导,但伞尖处不可微!
《生化危机》中保护伞公司的logo示意图
图中雨伞取1,2,3,4面合并为某一曲面,伞柄为Z轴向,假定两条黄虚线为x/y轴向。显然,伞尖处可偏导,但伞尖处不可微!
三、一阶偏导数连续与可微
灵魂之问2:为什么一阶偏导数连续,能推可微?反之则不成立?
上文说了一个道理,某点切平面可由共面的各方向导数构成。
类似的,某点切平面也可由共面的各连续偏导数构成。
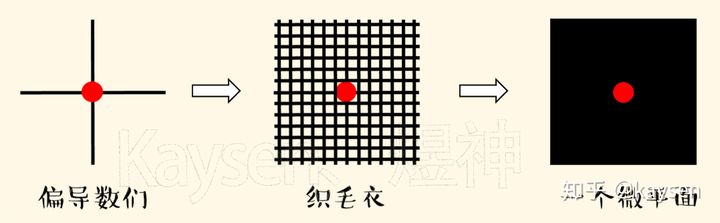 以偏导数为毛线,织毛衣,织出一个微平面
二者都可以构成那个切平面,来代表微曲面,只是形式不同而已。故一阶偏导连续,可推可微。
那可微为什么不能推出偏导连续?
把握二元曲面概念前,先弱化到一元曲线情景,曲线可微
以偏导数为毛线,织毛衣,织出一个微平面
二者都可以构成那个切平面,来代表微曲面,只是形式不同而已。故一阶偏导连续,可推可微。
那可微为什么不能推出偏导连续?
把握二元曲面概念前,先弱化到一元曲线情景,曲线可微 ![[公式]](https://www.zhihu.com/equation?tex=%5CRightarrow) 曲线光滑且连续(排除尖点),一阶导不连续。
则
曲线光滑且连续(排除尖点),一阶导不连续。
则 ![[公式]](https://www.zhihu.com/equation?tex=f%27%28x%29) 不存在,曲线为震荡函数!
这个结论何以成立?
煜神常在群里说的一个知识点是:若间断,则只有震荡间断点可能有原函数。那么
不存在,曲线为震荡函数!
这个结论何以成立?
煜神常在群里说的一个知识点是:若间断,则只有震荡间断点可能有原函数。那么 ![[公式]](https://www.zhihu.com/equation?tex=%EF%BC%88%E5%8E%9F%E5%87%BD%E6%95%B0%EF%BC%89%27) 出现间断,必定是震荡函数!
(P.S. 上句高能,请谨慎理解)
下面引出著名的震荡曲线:
出现间断,必定是震荡函数!
(P.S. 上句高能,请谨慎理解)
下面引出著名的震荡曲线:
![[公式]](https://www.zhihu.com/equation?tex=x%20%5Cne0%E6%97%B6%EF%BC%8Cy%3Dx%5E%7B2%7Dsin%5Cfrac%7B1%7D%7Bx%5E%7B2%7D%7D%20%3B)
![[公式]](https://www.zhihu.com/equation?tex=x%3D0%E6%97%B6%EF%BC%8Cy%3D0%2C)
感受震荡函数在原点附近的无穷魅力!

kaysen的视频
· 3678 播放
![[公式]](https://www.zhihu.com/equation?tex=x%3D0%2Cf%27%280%29%3D%5Clim_%7B%5CDelta%20x%20%5Crightarrow%200%7D%7B%5Cfrac%7B%5Cleft%28%20%5CDelta%20x%20%5Cright%29%20%5E%7B2%7Dsin%5Cfrac%7B1%7D%7B%5Cleft%28%20%5CDelta%20x%20%5Cright%29%20%5E%7B2%7D%7D%7D%7B%5CDelta%20x%7D%7D%3D0)
![[公式]](https://www.zhihu.com/equation?tex=x%5Cne0%2Cf%27%280%29%3D2xsin%5Cfrac%7B1%7D%7Bx%5E%7B2%7D%7D-%5Cfrac%7B2%7D%7Bx%7Dcos%5Cfrac%7B1%7D%7Bx%5E%7B2%7D%7D) ,无穷warning!
,无穷warning!
![[公式]](https://www.zhihu.com/equation?tex=f%28x%29) 可微,导数不连续。
我们将该曲线绕y轴旋转一周,将x,y同质化,得到二元震荡曲面,类似水波纹中心点的形态!函数式为:
可微,导数不连续。
我们将该曲线绕y轴旋转一周,将x,y同质化,得到二元震荡曲面,类似水波纹中心点的形态!函数式为:
![[公式]](https://www.zhihu.com/equation?tex=x%5E%7B2%7D%2By%5E%7B2%7D%20%5Cne0%E6%97%B6%EF%BC%8Cz%3D%28x%5E%7B2%7D%2By%5E%7B2%7D%29sin%5Cfrac%7B1%7D%7Bx%5E%7B2%7D%2By%5E%7B2%7D%7D%20%3B)
![[公式]](https://www.zhihu.com/equation?tex=x%5E%7B2%7D%2By%5E%7B2%7D%3D0%E6%97%B6%EF%BC%8Cz%3D0)
 上述二元震荡函数图像,可以近似作涟漪观想
在
上述二元震荡函数图像,可以近似作涟漪观想
在 ![[公式]](https://www.zhihu.com/equation?tex=%280%2C0%29) 点,
点, ![[公式]](https://www.zhihu.com/equation?tex=f%28x%2Cy%29) 显然可微(存在一个水平的切平面),但在
显然可微(存在一个水平的切平面),但在 ![[公式]](https://www.zhihu.com/equation?tex=%280%2C0%29) 点附近偏导不连续,存在无穷多个趋近竖直的切平面(由一元震荡函数在原点附近的“竖直”切线旋转而成)。无穷warning再次发生!
此处请思考悖论3:☠
既然上述函数在
点附近偏导不连续,存在无穷多个趋近竖直的切平面(由一元震荡函数在原点附近的“竖直”切线旋转而成)。无穷warning再次发生!
此处请思考悖论3:☠
既然上述函数在 ![[公式]](https://www.zhihu.com/equation?tex=%280%2C0%29) 点可微,且有一个水平的微平面。那么微平面又可由连续的一阶偏导所构成,这样一来不就表明函数就在
点可微,且有一个水平的微平面。那么微平面又可由连续的一阶偏导所构成,这样一来不就表明函数就在 ![[公式]](https://www.zhihu.com/equation?tex=%280%2C0%29) 点处一阶偏导连续了么?
学长释疑:✍
两个角度梳理,数理和极限本质!
First,先数理逻辑,
可微性的判别式为
点处一阶偏导连续了么?
学长释疑:✍
两个角度梳理,数理和极限本质!
First,先数理逻辑,
可微性的判别式为
![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7B%5Crho%20%5Crightarrow%200%7D%7B%5Cfrac%7B%5CDelta%20z%20-%20dy%7D%7B%5Crho%7D%7D%3D%5Clim_%7B%5Crho%20%5Crightarrow%200%7D%7B%5Cfrac%7B%5CDelta%20z-%5Cleft%5B%20f%27_%7Bx%7D%280%2C0%29%5CDelta%20x%2B%20f%27_%7By%7D%280%2C0%29%5CDelta%20y%20%5Cright%5D%7D%7B%5Crho%7D%7D%3D0) 其中,
其中, ![[公式]](https://www.zhihu.com/equation?tex=%5Crho%3D%5Csqrt%7B%28%5CDelta%20x%29%5E%7B2%7D%2B%28%5CDelta%20y%29%5E%7B2%7D%7D) 意思是,全增量(二元函数值的实际差值)与全微分(以直代曲下全增量的近似值)要足够接近到误差可以忽略不计。用上式计算
意思是,全增量(二元函数值的实际差值)与全微分(以直代曲下全增量的近似值)要足够接近到误差可以忽略不计。用上式计算![[公式]](https://www.zhihu.com/equation?tex=%280%2C0%29) 点处,判别式值为0,推出可微。
一阶偏导,计算如下
点处,判别式值为0,推出可微。
一阶偏导,计算如下
![[公式]](https://www.zhihu.com/equation?tex=x%5E%7B2%7D%2By%5E%7B2%7D%3D0%EF%BC%8Cf%27_%7Bx%7D%5Cleft%28%200%2C0%20%5Cright%29%3D%5Clim_%7B%5CDelta%20x%20%5Crightarrow%200%7D%7B%5Cfrac%7Bf%280%2B%5CDelta%20x%29-f%280%2C0%29%7D%7B%5CDelta%20x%7D%7D%3D%5Clim_%7B%5CDelta%20x%20%5Crightarrow%200%7D%7B%5CDelta%20x%20sin%5Cfrac%7B1%7D%7B%5CDelta%20x%5E%7B2%7D%7D%7D%3D0)
![[公式]](https://www.zhihu.com/equation?tex=x%5E%7B2%7D%2By%5E%7B2%7D%5Cne0%EF%BC%8Cf%27_%7Bx%7D%5Cleft%28%20x%2Cy%20%5Cright%29%3D2xsin%5Cfrac%7B1%7D%7Bx%5E2%2By%5E2%7D-%5Cfrac%7B2x%7D%7Bx%5E2%2By%5E2%7Dcos%5Cfrac%7B1%7D%7Bx%5E2%2By%5E2%7D) 后式仍震个不停,在原点处不连续。所以,可微推不出一阶偏导连续。
Second,极限本质角度!
该函数在
后式仍震个不停,在原点处不连续。所以,可微推不出一阶偏导连续。
Second,极限本质角度!
该函数在![[公式]](https://www.zhihu.com/equation?tex=%280%2C0%29) 点可微,是根据约定俗成的可微定义,计算出的近似结果。你可以认为原点处存在一个微平面,但实际上,它是极限思想制造出的幻象!
除了
点可微,是根据约定俗成的可微定义,计算出的近似结果。你可以认为原点处存在一个微平面,但实际上,它是极限思想制造出的幻象!
除了![[公式]](https://www.zhihu.com/equation?tex=%280%2C0%29) 点,周围任意方向都是震荡不止的原函数,暗流汹涌。只是越接近0,看上去越平静,故原点邻域内,可近似认为那块儿是个平面,也可微。
在振幅无穷小的
点,周围任意方向都是震荡不止的原函数,暗流汹涌。只是越接近0,看上去越平静,故原点邻域内,可近似认为那块儿是个平面,也可微。
在振幅无穷小的![[公式]](https://www.zhihu.com/equation?tex=%280%2C0%29) 点周围,一阶偏导由于震荡,存在无穷多个无穷大的偏导值。
它们近在咫尺,又远在天涯。间断的不清不楚,不明不白。
点周围,一阶偏导由于震荡,存在无穷多个无穷大的偏导值。
它们近在咫尺,又远在天涯。间断的不清不楚,不明不白。
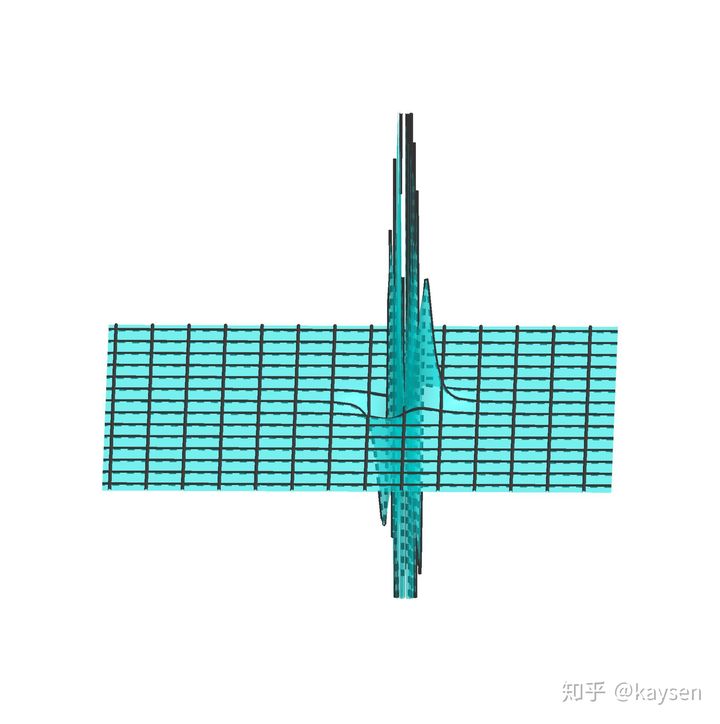 一阶偏导的图像,类似上海外滩-纽约曼哈顿的摩天大楼
至此,概念辩证End!
看了文章,再来回忆下这几组概念的辩证关系,是否能理解的更深刻一些?
一阶偏导的图像,类似上海外滩-纽约曼哈顿的摩天大楼
至此,概念辩证End!
看了文章,再来回忆下这几组概念的辩证关系,是否能理解的更深刻一些?

本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。