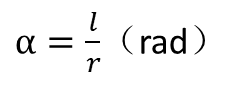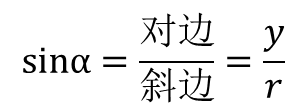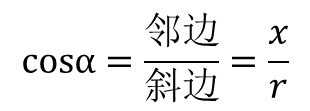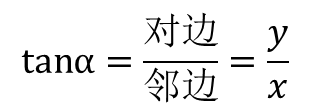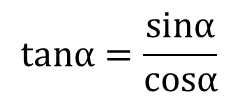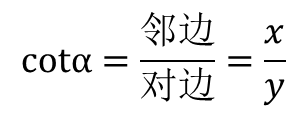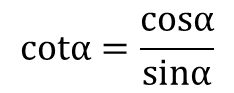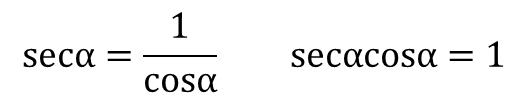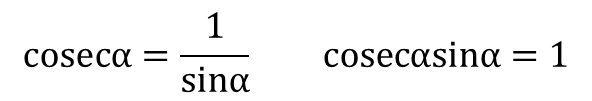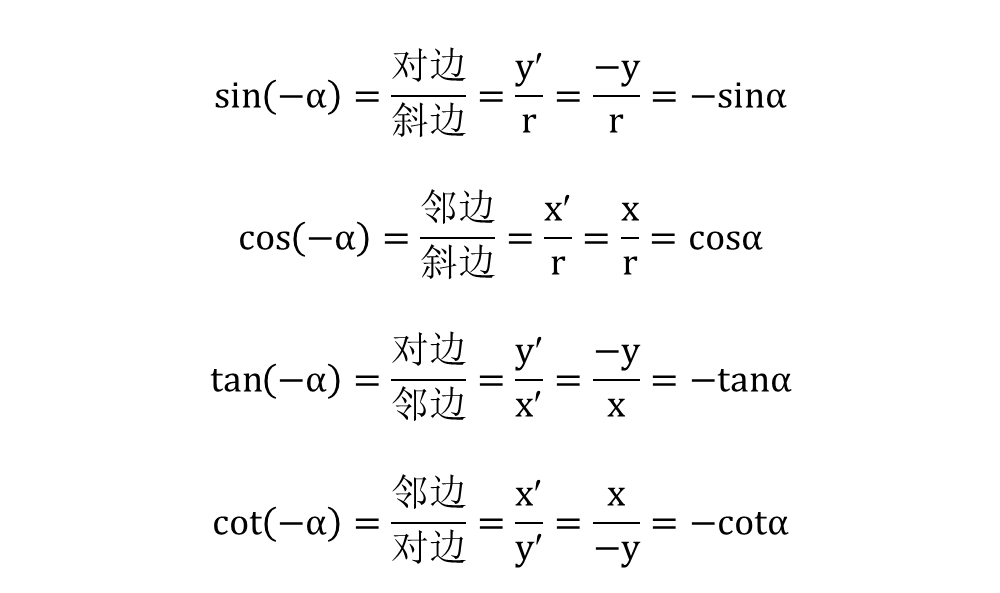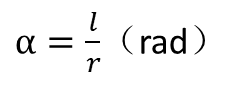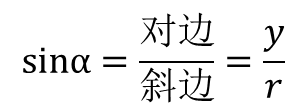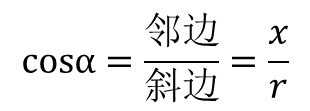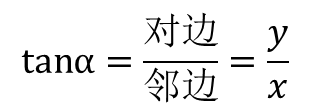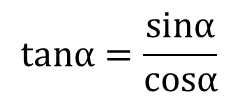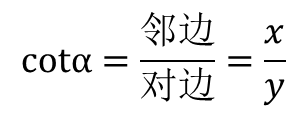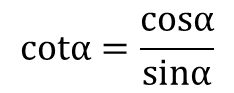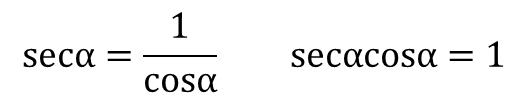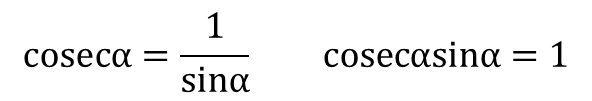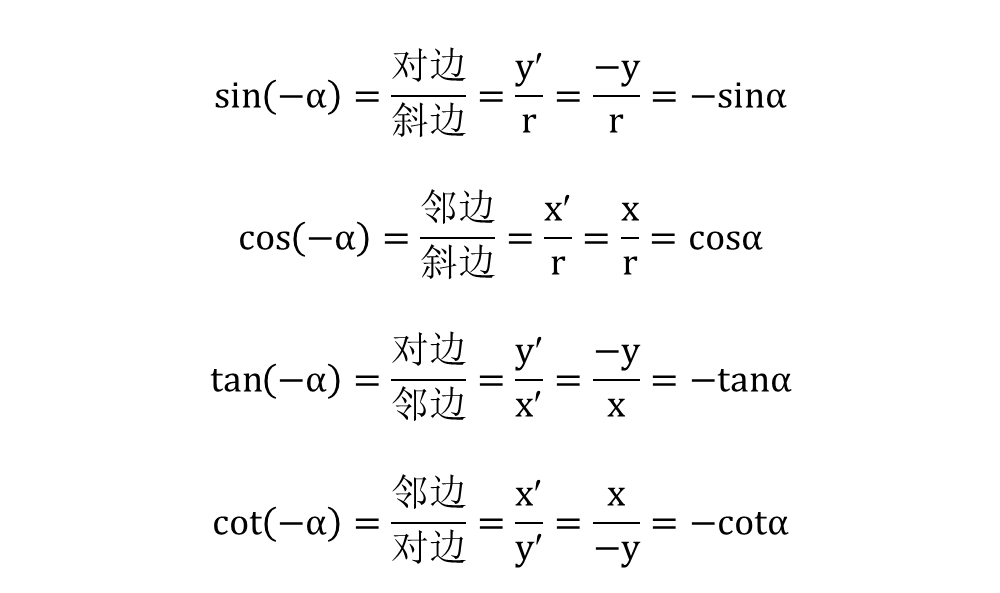三角函数是中学数学学习的重点、难点之一。有同学数学学习本来还不错,但从三角函数开始情况变得不再乐观,学习开始发懵,感觉到数学学习力不从心,学习成绩明显下滑:要么概念不能熟练掌握、不好理解;要么觉得公式太多,没办法背熟、记全;要么三角函数特殊角的数值大小、正负记不牢,容易混淆。因而,三角函数成为中学数学学习上的拦路虎,甚至成为部分学生的噩梦。
下面,以平面直角坐标系作为基础,从基本概念开始介绍,希望能够降低三角函数的学习难度,帮助大家更快更好地掌握三角函数。
一、 准备知识
1、 平面直角坐标系
如图1所示,建立平面直角坐标系xOy,坐标平面被x轴和y轴分割成四个部分,分别称做第一象限、第二象限、第三象限及第四象限。
图1平面直角坐标系
2、 角度正、负规定
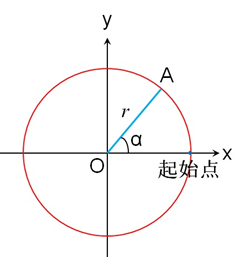
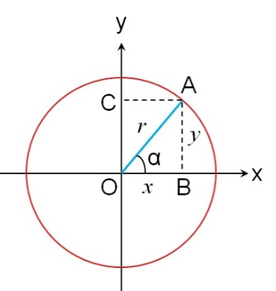
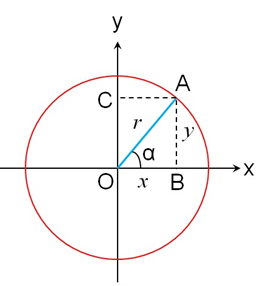
以平面直角坐标系原点O为圆心,做半径为r的圆,半径OA与x轴的夹角记为α,如图2所示。
图2
α角大小的变化,可以看做是A点以r为半径绕原点O转动所致,A点转动的起始位置在x轴上。
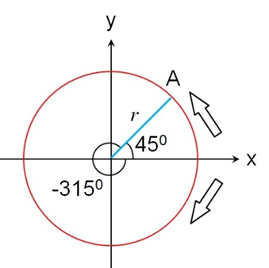
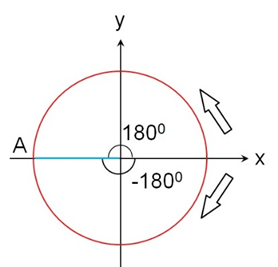
规定:从x轴指向半径OA,逆时针时α角为正值,顺时针时α角为负值。如图3所示,α=45度或者-315度;如图4所示,α=180度或者-180度。
图3
图4
3、 角度单位:弧度(rad)
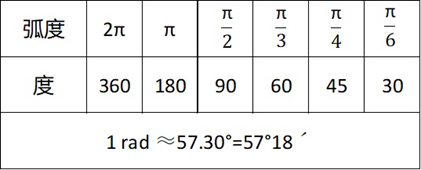
大家都知道,角度的常用单位是度,转一圈是360度,平角是180度,直角是90度。
俗话说入乡随俗,到哪道山唱什么歌。在数学、物理等学科,角度的单位一般不再用度,而是用弧度。弧度的英文词汇是radian,缩写成rad,不过人们习惯弧度的单位省略不写。
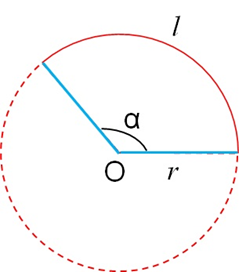
(1)弧度的定义:弧度制指对于一个圆,用弧长l与半径r之比来度量对应圆心角α角度的方式,如图5所示。
图5
(2)弧度与度的换算
根据弧度定义,等于半径长的圆弧所对的圆心角是1弧度;一个圆周长是2πr,其圆心角就是2π弧度,简称2π。弧度与度的换算关系如下:
弧度的精髓就在于它是一个与圆半径无关的量,从而大大简化了有关公式及运算。
4、 半径OA的投影
如图6所示,对于锐角α,A点位于第一象限,半径OA在x轴上的的投影为OB,长度记为x;半径OA在y轴上的的投影为OC,长度记为y,则三角形OBA构成直角三角形。
图6
二、 三角函数的基本定义
在直角三角形OBA中,直边x、y及斜边r与角α的基本关系有六种:正弦函数,余弦函数,正切函数,余切函数,正割函数,余割函数,常用的是前三种函数。
这六种函数的定义如下:
1、 正弦函数
在直角三角形中,锐角α的对边与斜边的比值,称做α角的正弦函数,简称α角的正弦,记作sinα(sin是正弦一词的英语词汇sine的缩写),即
从图6上可以看出,当α=0时, y=0,sinα=0,最小;当α=90度时,y=r,sinα=1,最大;所以sinα的取值范围有:0≤sinα≤1。
2、 余弦函数
在直角三角形中,锐角α的邻边与斜边的比值,称做α角的余弦函数,简称α角的余弦,记作cosα(cos是余弦一词的英语词汇cosine的缩写),即
从图6上可以看出,当α=0时,x=r,cosα=1,最大;当α=90度时,x=0,cosα=0,最小;所以cosα的取值范围有:0≤cosα≤1。
3、 正切函数
在直角三角形中,锐角α的对边与邻边的比值,称做α角的正切函数,简称α角的正切,记作tanα或tgα(tan、tg都是正切一词的英语词汇tangent的缩写),即
考虑到正弦函数、余弦函数的定义,得知
从图6上可以看出,当α=0时,x=r,y=0,tanα=0,最小;当α=90度时,x=0,y=r,tanα趋于无穷大,发散;所以tanα的取值范围有:0≤tanα<∞。
4、 余切函数
在直角三角形中,锐角α的邻边与对边的比值,称做α角的余切函数,简称α角的余切,记作cotα或ctgα(cot、ctg都是余切一词的英语词汇Cotangent的缩写),即
从定义上可以看出,余切是正切的倒数,有
考虑到正弦函数、余弦函数的定义,得知
从图6上也可以看出,当α=0时,x=r,y=0,cotα趋于无穷大,发散;当α=90度时,x=0,y=r,cotα=0,最小;所以cotα的取值范围有:0≤cotα<∞。
5、 正割函数
正割函数是余弦函数的倒数,是在直角三角形中,锐角α的斜边与邻边的比值,记作secα(sec是正割一词的英语词汇Secant的缩写),即
从图6上可以看出,当α=0时,x=r,secα=1,最小;当α=90度时,x=0,secα趋于无穷大,发散;所以cosα的取值范围有:1≤secα<∞。
6、 余割函数
余割函数是正弦函数的倒数,是在直角三角形中,锐角α的斜边与对边的比值,记作cosecα(cosec是正割一词的英语词汇Cosecant的缩写),即
从图6上可以看出,当α=0时, y=0,cosecα趋于无穷大,发散=0;当α=90度时,y=r,cosecα=1,最小;所以cosecα的取值范围有:1≤cosecα<∞。
三、 三角函数定义的扩展,诱导公式
上面有关三角函数的定义是对锐角而言的。其实,这个定义可以扩展到任意角度。
设任意角记为b,锐角记为α,则b角总归会化成如下形式之一:
b=2kπ±α,b=3π/2±α,b=π±α,b=π/2±α
其中k是A点转动的圈数。A点既可以逆时针转动,也可以顺时针转动,故k可正可负,有k=0, ±1, ±2,¼,即k∈Z。
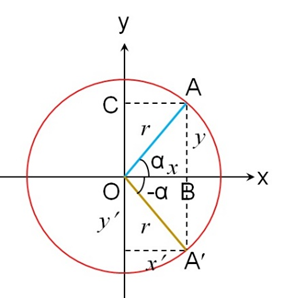
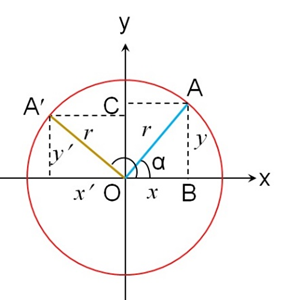
1、 负角(β=-α)的三角函数,如图7所示。
图7
从图7可以看出,半径OA撇在x轴上的投影x撇与x重合,在y轴上的投影y撇是负值,大小等于y。则有诱导公式(一)
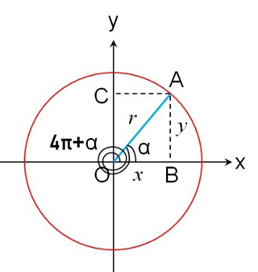
2、 β=2kπ+α的三角函数,如图8所示是k=2的情形。
图8
无论圆周上的A点绕O点转多少圈,只要终边OA处于同一位置,这些角的三角函数值不变。即诱导公式(二)
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot (2kπ+α)= cotα
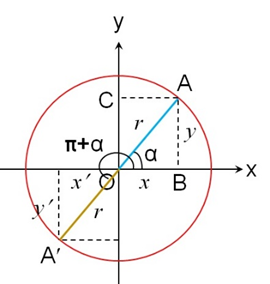
3、 β=π+α的三角函数,如图9所示。
图9
从图9可以看出,半径OA撇在x、y轴上的投影x撇、y撇均为负值,但其大小与半径OA的投影是一样的。则有诱导公式(三)
sin(π+α) =-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
4、 β=π/2+α的三角函数,如图10所示。
图10
从图10可以看出,半径OA撇在x轴上的投影x撇为负值,大小等于y; OA撇在y轴上的投影y撇是正值,大小等于x。则有诱导公式(四)
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
5、以上四组诱导公式是三角函数的基础公式,一定要根据所附图示熟练掌握。对于其余的b=2kπ-α,b=3π/2±α,b=π-α,b=π/2-α的三角函数可以由上面的四组诱导公式推导出来,不用死记硬背。
(1)诱导公式(五):b=2kπ-α的三角函数
角度2kπ-α可以看做是2kπ+(-α),联合使用公式(二)和(一),就可以得知
sin(2kπ-α)=sin(2kπ+(-α))=sin(-α)=-sinα
其余函数比葫芦画瓢既有
cos(2kπ-α)=cosα
tan(2kπ-α)=-tanα
cot(2kπ-α)=-cotα
(2)诱导公式(六):b=π-α的三角函数。
依照b=2kπ-α的做法,由诱导公式(三)以此类推。
sin(π-α) =sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
(3)诱导公式(七):b=π/2-α的三角函数
依照b=2kπ-α的做法,由诱导公式(四)以此类推。
sin(π/2-α)=cosα
cos(π/2-α)= sinα
tan(π/2-α)= cotα
cot(π/2-α)= tanα
(4)诱导公式(八):b=3π/2±α的三角函数
b=3π/2±α看成是b=π+(π/2±α),可以把π/2±α看做是锐角,就可以套用诱导公式(三),再用相应诱导公式(四)和(七)即可
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(3π/2-α) =-cosα
cos(3π/2-α) =-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)= tanα
从上面讨论可知,诱导公式中,α角不一定非为锐角不可,可以是任意角度。
四、 利用平面直角坐标系可以很直观地判断三角函数的正负、增减及奇偶性
1、三角函数的正负
(1) 在平面直角坐标系第一象限内,参考图11,OA的投影x、y皆为正。
图11
故根据定义,sinα、cosα、tanα、cotα的值皆为正。
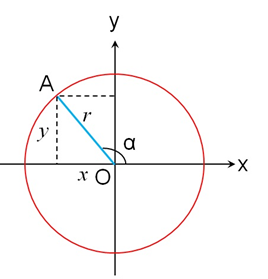
(2) 在平面直角坐标系第二象限内,参考图12,OA的投影x为负、y为正。
图12
故sinα为正,cosα、tanα、cotα皆为负。
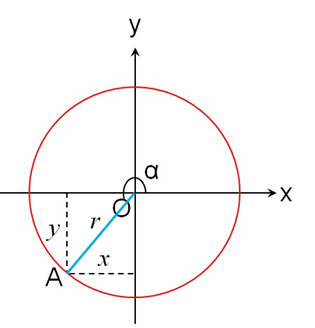
(3) 在平面直角坐标系第三象限内,参考图13,OA的投影x、y皆为负。
图13
故sinα、cosα为负,tanα、cotα为正。
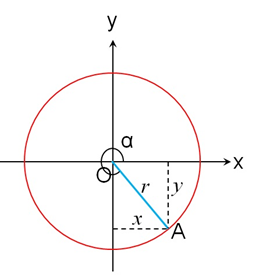
(4) 在平面直角坐标系第四象限内,参考图14,OA的投影x为正、y为负。
图14
故cosα为正,sinα、tanα、cotα皆为负。
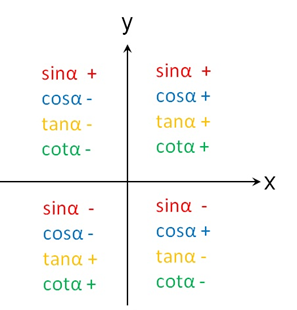
三角函数值正负规律总结如下(图15):
正弦函数sinα一二象限正,三四象限负;
余弦函数sinα一四象限正,二三象限负;
正切、余切函数tanα、cotα一三象限正,二四象限负。
图15 本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。