 序 本章的结构
第一节 熵的概念与熵变计算式①
第二节 热力学第三定律与绝对熵①
第三节 过程的可逆性与热力学第二定律②
第四节 熵增原理,赫姆霍兹函数与吉布斯函数②
第五节 热力学基本方程,麦克斯韦关系式③
第六节 热力学公式证明与热力学计算③
第七节 磁功问题热力学/绝热去磁降温③
序 本章的结构
第一节 熵的概念与熵变计算式①
第二节 热力学第三定律与绝对熵①
第三节 过程的可逆性与热力学第二定律②
第四节 熵增原理,赫姆霍兹函数与吉布斯函数②
第五节 热力学基本方程,麦克斯韦关系式③
第六节 热力学公式证明与热力学计算③
第七节 磁功问题热力学/绝热去磁降温③
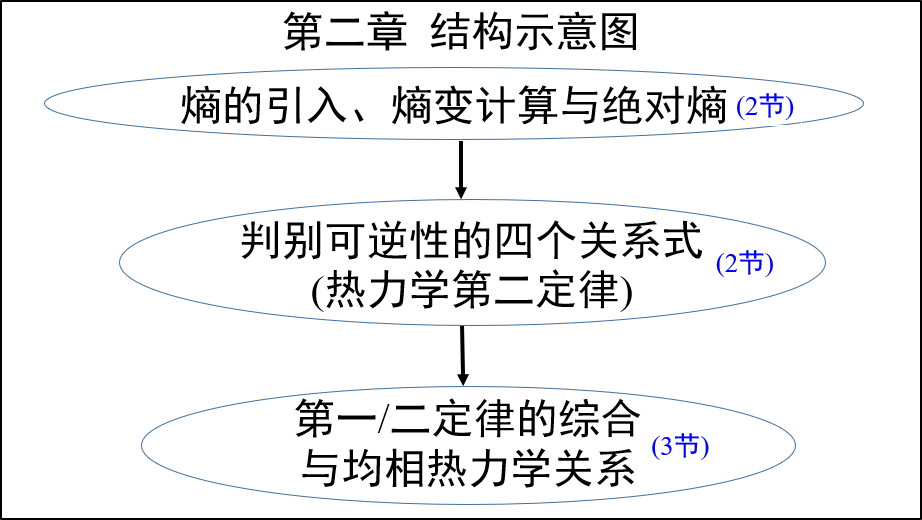 与大多数教材不同,视频“熵概念的背景与简单引出”用非常简单的方式引入熵,而不是采用常见的、借助卡诺循环的方式。熵概念简单、快速的引入,为接下来的熵变计算奠定基础。这两种教学策略的对比分析,见视频“第一部分回顾总结”。视频“热力学基本方程的适用条件”中,不但给出了适用条件,而且分析了每一个条件的来源。对比发现,很多教材缺乏来源分析,特别是均相的来源分析。熵变计算的展开,沿用了基本过程与组合的思想,它是贯穿整个热力学的基本思想。
与大多数教材不同,视频“熵概念的背景与简单引出”用非常简单的方式引入熵,而不是采用常见的、借助卡诺循环的方式。熵概念简单、快速的引入,为接下来的熵变计算奠定基础。这两种教学策略的对比分析,见视频“第一部分回顾总结”。视频“热力学基本方程的适用条件”中,不但给出了适用条件,而且分析了每一个条件的来源。对比发现,很多教材缺乏来源分析,特别是均相的来源分析。熵变计算的展开,沿用了基本过程与组合的思想,它是贯穿整个热力学的基本思想。



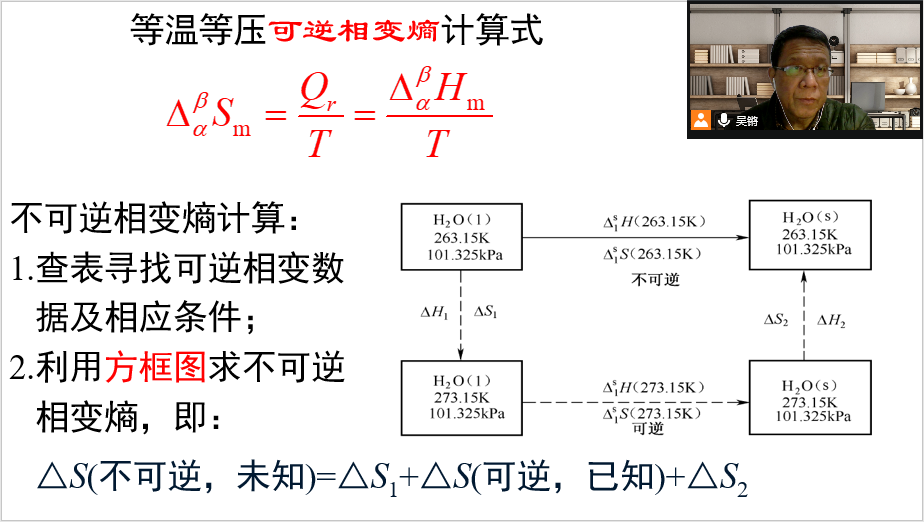
 1.根据状态函数理论,就已经知道U=U(S, V),因此有关于U的全微分dU。请问通过函数U=U(S, V)得到的全微分dU,与公式dU=TdS-pdV有怎样的关系?
2.热力学基本定律的适用条件之一,是“没有非体积功”。请问如果体积功存在的同时,还有非体积功,热力学基本定律会变成怎样?
3.状态函数理论指出:没有非体积功时,状态函数之间通常具有二元函数关系。请问二元函数(而不是一元函数或三元函数)关系与热力学基本方程有什么内在联系?
4.混合过程有热容概念吗?为什么?
5.对于任何纯物质,△S熔化明显小于△S蒸发。请问该结论对不纯的物质是否成立?为什么?
视频“热力学第三定律”中,借助基本过程分类,指出了化学反应的熵变计算,相对于其他三种基本过程熵变计算的特殊性,进而通过与生成焓概念类比,引发绝对熵概念。视频“熵值最小状态的寻找与规定”中,第四个基本过程(混合过程)的重要性得以体现,因为绝对熵为零要求的纯物质的“纯”,就源于混合概念;完美晶体的“完美”,本质上也源于混合概念。此外,我们第一次将化合物生成焓与Nernst热定理联系起来。视频“第一部分回顾总结”中,介绍了应对教学难点的一个具体策略,即分解难点,把热力学第二定律分解为熵变计算与熵变概念应用两个部分。同时,从三个方面具体体现“以学生为中心”的教学理念。该视频还介绍了争议问题的磋商方法,这对物理化学中有争议、不易说清楚问题的澄清,很有帮助。
1.根据状态函数理论,就已经知道U=U(S, V),因此有关于U的全微分dU。请问通过函数U=U(S, V)得到的全微分dU,与公式dU=TdS-pdV有怎样的关系?
2.热力学基本定律的适用条件之一,是“没有非体积功”。请问如果体积功存在的同时,还有非体积功,热力学基本定律会变成怎样?
3.状态函数理论指出:没有非体积功时,状态函数之间通常具有二元函数关系。请问二元函数(而不是一元函数或三元函数)关系与热力学基本方程有什么内在联系?
4.混合过程有热容概念吗?为什么?
5.对于任何纯物质,△S熔化明显小于△S蒸发。请问该结论对不纯的物质是否成立?为什么?
视频“热力学第三定律”中,借助基本过程分类,指出了化学反应的熵变计算,相对于其他三种基本过程熵变计算的特殊性,进而通过与生成焓概念类比,引发绝对熵概念。视频“熵值最小状态的寻找与规定”中,第四个基本过程(混合过程)的重要性得以体现,因为绝对熵为零要求的纯物质的“纯”,就源于混合概念;完美晶体的“完美”,本质上也源于混合概念。此外,我们第一次将化合物生成焓与Nernst热定理联系起来。视频“第一部分回顾总结”中,介绍了应对教学难点的一个具体策略,即分解难点,把热力学第二定律分解为熵变计算与熵变概念应用两个部分。同时,从三个方面具体体现“以学生为中心”的教学理念。该视频还介绍了争议问题的磋商方法,这对物理化学中有争议、不易说清楚问题的澄清,很有帮助。
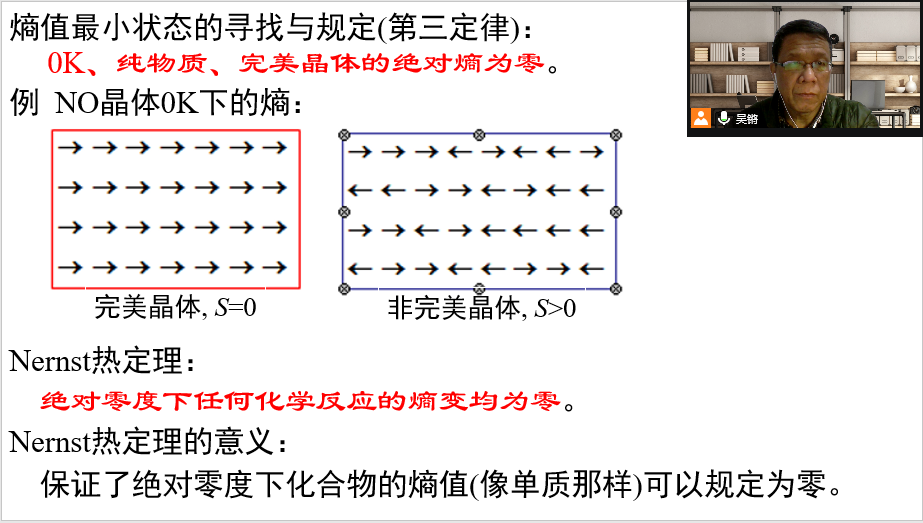



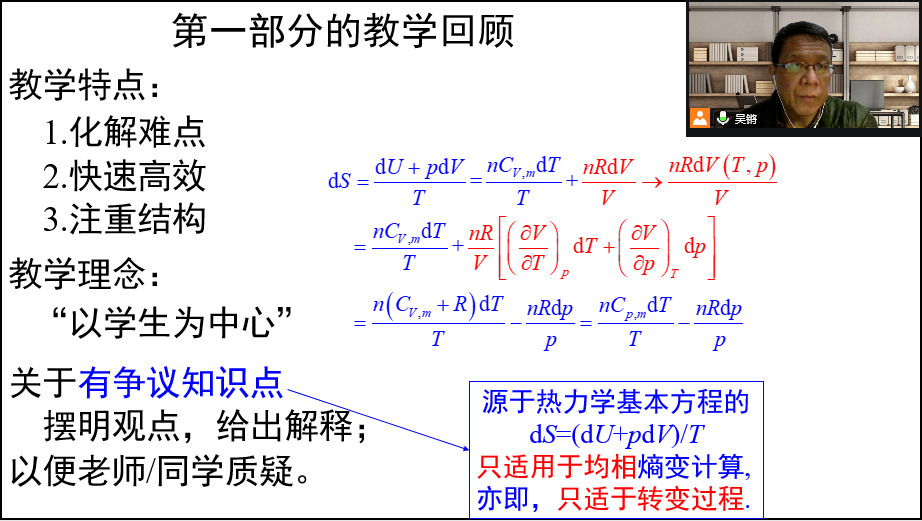 1.在298K与1atm下,石墨的摩尔熵大于金刚石的摩尔熵。请问在绝对零度下,石墨与金刚石的摩尔熵还有差别吗?视频“过程的可逆性”中,我们把平衡过程、准静态过程与可逆过程三个概念放在一起,它们的集中分析,有助于认清过程可逆性的本质。视频“第二定律的数学表达式”中,有不少值得看的“新”内容,如将过程四要素概念应用到克劳修斯不等式的解释,进而严格界定了反向过程,它对澄清“非自发”概念很有帮助。
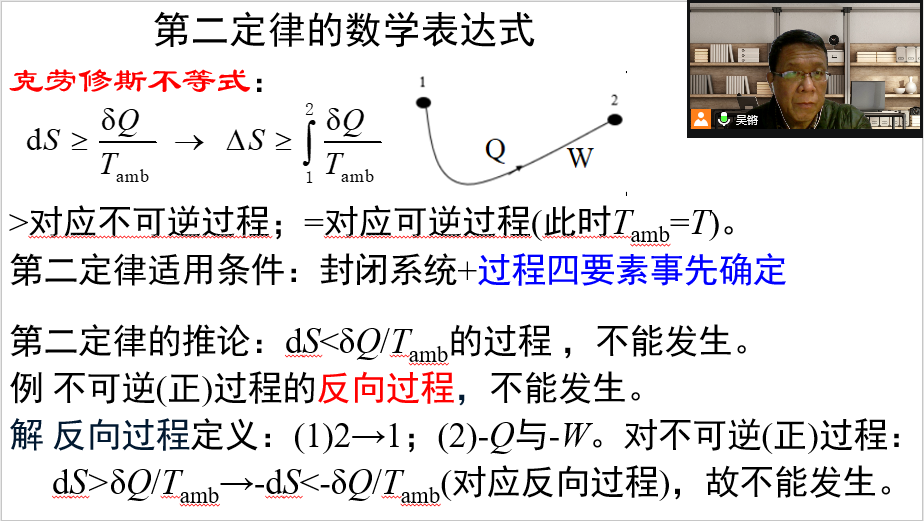
1.在298K与1atm下,石墨的摩尔熵大于金刚石的摩尔熵。请问在绝对零度下,石墨与金刚石的摩尔熵还有差别吗?视频“过程的可逆性”中,我们把平衡过程、准静态过程与可逆过程三个概念放在一起,它们的集中分析,有助于认清过程可逆性的本质。视频“第二定律的数学表达式”中,有不少值得看的“新”内容,如将过程四要素概念应用到克劳修斯不等式的解释,进而严格界定了反向过程,它对澄清“非自发”概念很有帮助。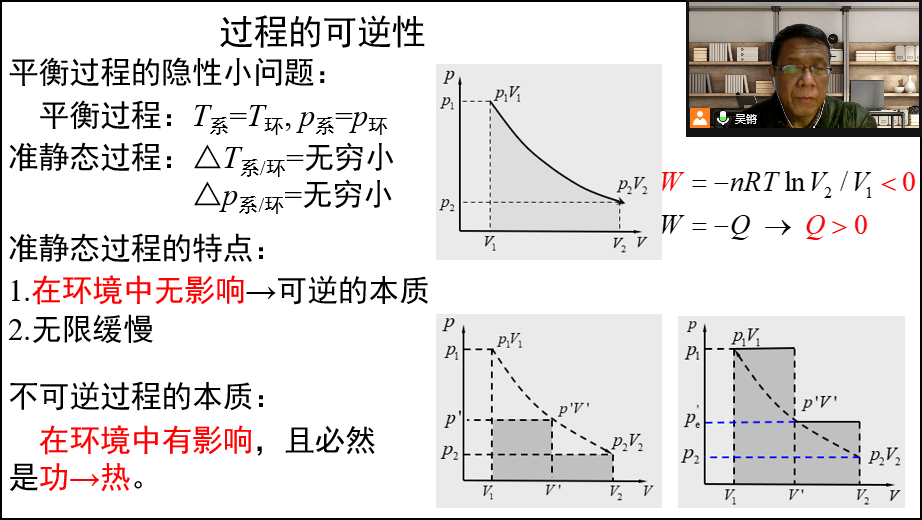
 视频“熵增原理”中,明确指出了热力学范畴内不存在自发/自动的概念。换言之,热力学第二定律与自发/自动无关!视频“亥姆霍兹函数A”中,基于两个过程量计算方便的差异,介绍了亥姆霍兹判据,这一教学思路尚未见过。视频“吉布斯函数(自由能)”中,区分了dG=0与δG=0,前者针对过程,后者针对状态;前者是吉布斯函数判据的直接结论,后者则是该判据的推论。视频“两个教学问题的说明”中,进一步阐述了为什么“自发/非自发”概念不属于热力学范畴。这是一个争议颇大的问题。鉴于此,视频中建议了讨论该问题的方式,因为经验表明,微信群中随机讨论的方式,根本无法应对这类复杂的问题。另外,对基本物理定律的教学策略做了概括总结。
视频“熵增原理”中,明确指出了热力学范畴内不存在自发/自动的概念。换言之,热力学第二定律与自发/自动无关!视频“亥姆霍兹函数A”中,基于两个过程量计算方便的差异,介绍了亥姆霍兹判据,这一教学思路尚未见过。视频“吉布斯函数(自由能)”中,区分了dG=0与δG=0,前者针对过程,后者针对状态;前者是吉布斯函数判据的直接结论,后者则是该判据的推论。视频“两个教学问题的说明”中,进一步阐述了为什么“自发/非自发”概念不属于热力学范畴。这是一个争议颇大的问题。鉴于此,视频中建议了讨论该问题的方式,因为经验表明,微信群中随机讨论的方式,根本无法应对这类复杂的问题。另外,对基本物理定律的教学策略做了概括总结。


 1.请总结亥姆霍兹判据和吉布斯判据的推导思路。
2.无论亥姆霍兹判据还是吉布斯判据,请你根据推导过程说明:它们不仅仅适用于单相系统,也适用于多相系统。
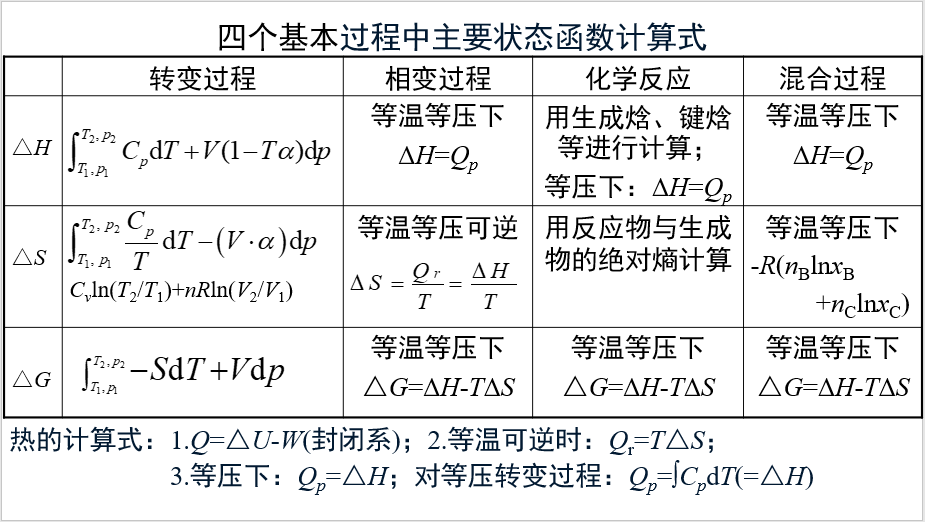
在下面的几个视频中,强调了热力学基本方程与麦克斯韦关系式等,仅适用于均相的转变过程。换言之,这些公式的适用范围并不大,在相变、化学反应与混合这三个基本过程中,不能使用这些公式!变量替换的视频共三个,目的是简化热力学推导,因为很多推导已经包含着其中了。
1.请总结亥姆霍兹判据和吉布斯判据的推导思路。
2.无论亥姆霍兹判据还是吉布斯判据,请你根据推导过程说明:它们不仅仅适用于单相系统,也适用于多相系统。
在下面的几个视频中,强调了热力学基本方程与麦克斯韦关系式等,仅适用于均相的转变过程。换言之,这些公式的适用范围并不大,在相变、化学反应与混合这三个基本过程中,不能使用这些公式!变量替换的视频共三个,目的是简化热力学推导,因为很多推导已经包含着其中了。




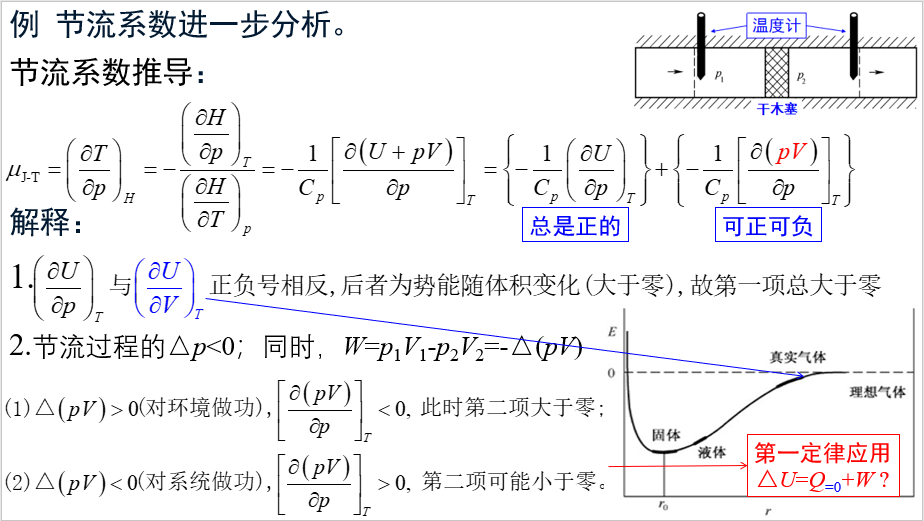
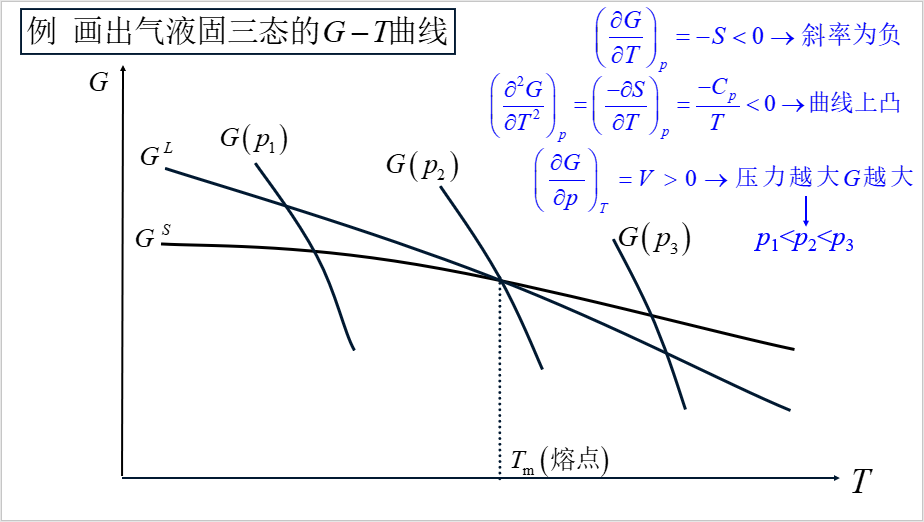
 视频“Gibbs-Helmholtz公式与背后的概念”看似简单,其隐含的概念值得关注。视频“例 节流系数进一步分析”中,有一处非常特别的地方,即正面诠释了pV的含义,而通常情况下,只有p△V有意义。视频“例 画出三态G-T曲线”中,强调了热力学推导与曲线形状之间的关系。这是一大类问题的代表,因此本例具有普遍意义。
视频“Gibbs-Helmholtz公式与背后的概念”看似简单,其隐含的概念值得关注。视频“例 节流系数进一步分析”中,有一处非常特别的地方,即正面诠释了pV的含义,而通常情况下,只有p△V有意义。视频“例 画出三态G-T曲线”中,强调了热力学推导与曲线形状之间的关系。这是一大类问题的代表,因此本例具有普遍意义。



 这个部分尽管仅有三屏,且只讨论一个问题,但其意义很大。首先,突破了体积功的“一统天下”,让学生了解到体积功之外还有更为广阔、有用的新热力学体系;其次,从教学角度看,这里又一次采用了温故而知新的策略,因此教学效率比较高。要注意,教学效率是一个很少涉及的领域,它完全有可能成为物理化学教学改革的新方向!
这个部分尽管仅有三屏,且只讨论一个问题,但其意义很大。首先,突破了体积功的“一统天下”,让学生了解到体积功之外还有更为广阔、有用的新热力学体系;其次,从教学角度看,这里又一次采用了温故而知新的策略,因此教学效率比较高。要注意,教学效率是一个很少涉及的领域,它完全有可能成为物理化学教学改革的新方向!

 1.在S-T图上做一条闭合曲线,该闭合曲线所包围的面积有什么物理含义?注意:要按顺时针沿该曲线变化与逆时针两种情况进行分析。
2.磁功问题中,请判断等温下熵S对磁场强度H求偏导数的正负,并给予解释。提示:可以借助磁功问题的麦克斯韦关系式。
3.对于磁功问题,请画出GH-T曲线和GH-H曲线。 GH-H曲线与体积功问题的G-p曲线有什么差异?注意:GH是磁功问题的吉布斯函数。
1.在S-T图上做一条闭合曲线,该闭合曲线所包围的面积有什么物理含义?注意:要按顺时针沿该曲线变化与逆时针两种情况进行分析。
2.磁功问题中,请判断等温下熵S对磁场强度H求偏导数的正负,并给予解释。提示:可以借助磁功问题的麦克斯韦关系式。
3.对于磁功问题,请画出GH-T曲线和GH-H曲线。 GH-H曲线与体积功问题的G-p曲线有什么差异?注意:GH是磁功问题的吉布斯函数。
本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。











































































