这里就不涉及到严格的极限的定义,因为高中数学的课本中没有讲到极限的定义。
先来讲一个简单的概念:不定式。
设我们有两个函数 ![[公式]](https://www.zhihu.com/equation?tex=f%28x%29) 和
和 ![[公式]](https://www.zhihu.com/equation?tex=g%28x%29) ,若当
,若当 ![[公式]](https://www.zhihu.com/equation?tex=x%3Dx_0) 时,有
时,有 ![[公式]](https://www.zhihu.com/equation?tex=f%28x_0%29%3Dg%28x_0%29%3D0) ,则称分式
,则称分式 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf%28x_0%29%7D%7Bg%28x_0%29%7D) 为
为 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B0%7D%7B0%7D) 型不定式;
同样地,若当
型不定式;
同样地,若当 ![[公式]](https://www.zhihu.com/equation?tex=x%5Crightarrow+x_0) 时, 有
时, 有![[公式]](https://www.zhihu.com/equation?tex=f%28x%29%5Crightarrow+%5Cinfty) 并且
并且 ![[公式]](https://www.zhihu.com/equation?tex=g%28x%29%5Crightarrow%5Cinfty) (这里的无穷大可正可负)则称分式
(这里的无穷大可正可负)则称分式 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf%28x_0%29%7D%7Bg%28x_0%29%7D) 为
为 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%5Cinfty%7D%7B%5Cinfty%7D) 型不定式。
上面便是洛必达法则使用的前提条件,只有在满足条件时才能“洛”。
洛必达法则的内容如下,分为
型不定式。
上面便是洛必达法则使用的前提条件,只有在满足条件时才能“洛”。
洛必达法则的内容如下,分为 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B0%7D%7B0%7D) 型不定式和
型不定式和 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%5Cinfty%7D%7B%5Cinfty%7D) 型不定式。
定理1 (
型不定式。
定理1 ( ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B0%7D%7B0%7D) 型不定式)若当
型不定式)若当 ![[公式]](https://www.zhihu.com/equation?tex=x%3Dx_0) 时,
时, ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf%28x_0%29%7D%7Bg%28x_0%29%7D) 为
为 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B0%7D%7B0%7D) 型不定式,
型不定式, ![[公式]](https://www.zhihu.com/equation?tex=f%27%28x_0%29) 和
和 ![[公式]](https://www.zhihu.com/equation?tex=g%27%28x_0%29) 存在,且
存在,且 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf%27%28x_0%29%7D%7Bg%27%28x_0%29%7D) 不是不定式,则
不是不定式,则 ![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx%5Crightarrow+x_0%7D%5Cfrac%7Bf%28x%29%7D%7Bg%28x%29%7D%3D%5Cfrac%7Bf%27%28x%29%7D%7Bg%27%28x%29%7D) ;
定理2 (
;
定理2 ( ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%5Cinfty%7D%7B%5Cinfty%7D) 型不定式) 若当
型不定式) 若当 ![[公式]](https://www.zhihu.com/equation?tex=x%5Crightarrow+x_0) 时,
时, ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf%28x_0%29%7D%7Bg%28x_0%29%7D) 为
为 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%5Cinfty%7D%7B%5Cinfty%7D) 型不定式,
型不定式, ![[公式]](https://www.zhihu.com/equation?tex=f%27%28x_0%29) 和
和 ![[公式]](https://www.zhihu.com/equation?tex=g%27%28x_0%29) 存在,且
存在,且 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf%27%28x_0%29%7D%7Bg%27%28x_0%29%7D) 不是不定式,则
不是不定式,则 ![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx%5Crightarrow+x_0%7D%5Cfrac%7Bf%28x%29%7D%7Bg%28x%29%7D%3D%5Cfrac%7Bf%27%28x%29%7D%7Bg%27%28x%29%7D) 。
要解释这个定理,只需要用到导数的定义。
(需要注意的是,在这里我用的字眼是“解释”而不是“证明”,希望大家不要有着“证明就可以用”的念头。)
先考虑定理1,根据导数的定义,
。
要解释这个定理,只需要用到导数的定义。
(需要注意的是,在这里我用的字眼是“解释”而不是“证明”,希望大家不要有着“证明就可以用”的念头。)
先考虑定理1,根据导数的定义, ![[公式]](https://www.zhihu.com/equation?tex=f%27%28x_0%29%3D%5Clim_%7Bx%5Crightarrow+x_0%7D%5Cfrac%7Bf%28x%29-f%28x_0%29%7D%7Bx-x_0%7D) 。
则
。
则 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf%27%28x_0%29%7D%7Bg%27%28x_0%29%7D%3D%5Cfrac%7B%5Cdfrac%7Bf%28x%29-f%28x_0%29%7D%7Bx-x_0%7D%7D%7B%5Cdfrac%7Bg%28x%29-g%28x_0%29%7D%7Bx-x_0%7D%7D%3D%5Cfrac%7Bf%28x%29-f%28x_0%29%7D%7Bg%28x%29-g%28x_0%29%7D) ,其中
,其中 ![[公式]](https://www.zhihu.com/equation?tex=x%5Crightarrow+x_0) ,又根据
,又根据 ![[公式]](https://www.zhihu.com/equation?tex=f%28x_0%29%3Dg%28x_0%29%3D0) ,代入后即可得到
,代入后即可得到 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf%27%28x_0%29%7D%7Bg%27%28x_0%29%7D%3D%5Clim_%7Bx%5Crightarrow+x_0%7D%5Cfrac%7Bf%28x%29%7D%7Bg%28x%29%7D) ,即为所求结果。
再考虑定理2,当
,即为所求结果。
再考虑定理2,当 ![[公式]](https://www.zhihu.com/equation?tex=x%5Crightarrow+x_0) 时,若
时,若 ![[公式]](https://www.zhihu.com/equation?tex=f%28x%29%5Crightarrow+%5Cinfty) ,则
,则 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B1%7D%7Bf%28x%29%7D%5Crightarrow+0) ,记
,记 ![[公式]](https://www.zhihu.com/equation?tex=f_1%28x%29%3D%5Cfrac%7B1%7D%7Bf%28x%29%7D) ,
, ![[公式]](https://www.zhihu.com/equation?tex=g_1%28x%29%3D%5Cfrac%7B1%7D%7Bg%28x%29%7D) ,则
,则 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf_1%28x_0%29%7D%7Bg_1%28x_0%29%7D) 是
是 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B0%7D%7B0%7D) 型不定式,对其应用定理1得:
型不定式,对其应用定理1得:
![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx%5Crightarrow+x_0%7D%5Cfrac%7Bf_1%28x%29%7D%7Bg_1%28x%29%7D%3D%5Cfrac%7Bf%27_1%28x%29%7D%7Bg%27_1%28x%29%7D%3D%5Cfrac%7Bg%5E2%28x_0%29%7D%7Bf%5E2%28x_0%29%7D%5Ccdot+%5Cfrac%7Bf%27%28x_0%29%7D%7Bg%27%28x_0%29%7D) ,另一方面有
,另一方面有 ![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx%5Crightarrow+x_0%7D%5Cfrac%7Bf_1%28x%29%7D%7Bg_1%28x%29%7D%3D%5Cfrac%7Bg%28x_0%29%7D%7Bf%28x_0%29%7D) ,由此解得
,由此解得 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf%28x_0%29%7D%7Bg%28x_0%29%7D%3D%5Cfrac%7Bf%27%28x_0%29%7D%7Bg%27%28x_0%29%7D) ,也即
,也即 ![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx%5Crightarrow+x_0%7D%5Cfrac%7Bf%28x%29%7D%7Bg%28x%29%7D%3D%5Cfrac%7Bf%27%28x%29%7D%7Bg%27%28x%29%7D) 。
至此,便可以(不严谨地)说明上面的结论成立。
。
至此,便可以(不严谨地)说明上面的结论成立。
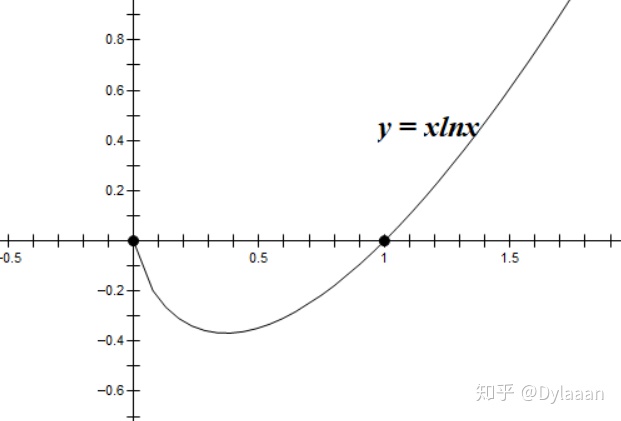
![[公式]](https://www.zhihu.com/equation?tex=y%3Dx%5Cln+x) 的图像。
解答 求导得
的图像。
解答 求导得 ![[公式]](https://www.zhihu.com/equation?tex=y%27%3D%5Cln+x%2B1) ,因此
,因此 ![[公式]](https://www.zhihu.com/equation?tex=y) 在
在 ![[公式]](https://www.zhihu.com/equation?tex=%280%2C%5Cfrac%7B1%7D%7Be%7D%29) 递减,在
递减,在 ![[公式]](https://www.zhihu.com/equation?tex=%28%5Cfrac%7B1%7D%7Be%7D%2C%2B%5Cinfty%29) 递增。
计算得
递增。
计算得 ![[公式]](https://www.zhihu.com/equation?tex=y%7C_%7Bx%3D%5Cfrac%7B1%7D%7Be%7D%7D%3D-%5Cfrac%7B1%7D%7Be%7D) ,
, ![[公式]](https://www.zhihu.com/equation?tex=y%7C_%7Bx%3D1%7D%3D0) ,接下来只需分析当
,接下来只需分析当 ![[公式]](https://www.zhihu.com/equation?tex=x%5Crightarrow+0) 时
时 ![[公式]](https://www.zhihu.com/equation?tex=y) 的取值。
的取值。
![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx%5Crightarrow+0%7Dx%5Cln+x%3D%5Clim_%7Bx%5Crightarrow+0%7D+%5Cfrac%7B%5Cln+x%7D%7B%5Cdfrac%7B1%7D%7Bx%7D%7D) ,此时发现
,此时发现 ![[公式]](https://www.zhihu.com/equation?tex=%5Cln+x) 和
和 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B1%7D%7Bx%7D) 都趋于无穷大,使用洛必达法则得:
都趋于无穷大,使用洛必达法则得:
![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx%5Crightarrow+0%7D+%5Cfrac%7B%5Cln+x%7D%7B%5Cdfrac%7B1%7D%7Bx%7D%7D%3D%5Clim_%7Bx%5Crightarrow+0%7D+%5Cfrac%7B%5Cdfrac%7B1%7D%7Bx%7D%7D%7B-%5Cdfrac%7B1%7D%7Bx%5E2%7D%7D%3D%5Clim_%7Bx%5Crightarrow+0%7D%28-x%29%3D0) ,因此
,因此 ![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx%5Crightarrow+0%7Dx%5Cln+x%3D0) 。
。
![[公式]](https://www.zhihu.com/equation?tex=x%3E0) 时,不等式
时,不等式 ![[公式]](https://www.zhihu.com/equation?tex=e%5Ex%5Cgeq+ax%2B1) 恒成立,求实数
恒成立,求实数 ![[公式]](https://www.zhihu.com/equation?tex=a) 的取值范围。
解答 分离参数得
的取值范围。
解答 分离参数得 ![[公式]](https://www.zhihu.com/equation?tex=a%5Cle+%5Cfrac%7Be%5Ex-1%7D%7Bx%7D) ,令
,令 ![[公式]](https://www.zhihu.com/equation?tex=f%28x%29%3D%5Cfrac%7Be%5Ex-1%7D%7Bx%7D) ,其中
,其中 ![[公式]](https://www.zhihu.com/equation?tex=x%3E0) 。
。
![[公式]](https://www.zhihu.com/equation?tex=f+%27%28x%29%3D%5Cfrac%7B%28x-1%29e%5Ex%2B1%7D%7Bx%5E2%7D) ,令
,令 ![[公式]](https://www.zhihu.com/equation?tex=g%28x%29%3D%28x-1%29e%5Ex%2B1) ,
, ![[公式]](https://www.zhihu.com/equation?tex=g%27%28x%29%3Dxe%5Ex%3E0) ,因此
,因此 ![[公式]](https://www.zhihu.com/equation?tex=g%28x%29) 在
在 ![[公式]](https://www.zhihu.com/equation?tex=%280%2C%2B%5Cinfty%29) 单调递增,
单调递增, ![[公式]](https://www.zhihu.com/equation?tex=g%28x%29%3E+g%280%29%3D0) ,因此
,因此 ![[公式]](https://www.zhihu.com/equation?tex=f%27%28x%29%3E0) ,
, ![[公式]](https://www.zhihu.com/equation?tex=f%28x%29) 在
在 ![[公式]](https://www.zhihu.com/equation?tex=%280%2C%2B%5Cinfty%29) 单调递增。
要求
单调递增。
要求 ![[公式]](https://www.zhihu.com/equation?tex=a%5Cle+f%28x%29) 恒成立,因此
恒成立,因此 ![[公式]](https://www.zhihu.com/equation?tex=a%5Cle+f%28x%29_%7Bmin%7D) ,但当
,但当 ![[公式]](https://www.zhihu.com/equation?tex=x%3D0) 时,
时, ![[公式]](https://www.zhihu.com/equation?tex=e%5Ex-1%3Dx%3D0) ,此即为
,此即为 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B0%7D%7B0%7D) 型不定式。根据洛必达法则,有:
型不定式。根据洛必达法则,有:
![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx+%5Crightarrow+0%7D%7B%5Cfrac%7Be%5Ex-1%7D%7Bx%7D%7D%3D%5Clim_%7Bx+%5Crightarrow+0%7D%7B%5Cfrac%7Be%5Ex%7D%7B1%7D%7D%3D1) ,因此
,因此 ![[公式]](https://www.zhihu.com/equation?tex=a%5Cle+1) ,实数
,实数 ![[公式]](https://www.zhihu.com/equation?tex=a) 的取值范围是
的取值范围是 ![[公式]](https://www.zhihu.com/equation?tex=%28-%5Cinfty+%2C1%5D) 。
例3 当
。
例3 当 ![[公式]](https://www.zhihu.com/equation?tex=x%3E0) 时,不等式
时,不等式 ![[公式]](https://www.zhihu.com/equation?tex=a+x%5Cgeq+%5Csin+x) 恒成立,求实数
恒成立,求实数 ![[公式]](https://www.zhihu.com/equation?tex=a) 的取值范围。
解答
的取值范围。
解答 ![[公式]](https://www.zhihu.com/equation?tex=%5CLeftrightarrow+a%5Cgeq+%5Cfrac%7B%5Csin+x%7D%7Bx%7D) ,又
,又 ![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx+%5Crightarrow+0%7D%7B%5Cfrac%7B%5Csin+x%7D%7Bx%7D%7D%3D%5Clim_%7Bx+%5Crightarrow+0%7D%7B%5Cfrac%7B%5Ccos+x%7D%7B1%7D%7D%3D1) ,因此
,因此 ![[公式]](https://www.zhihu.com/equation?tex=a%5Cgeq+1) 。
当
。
当 ![[公式]](https://www.zhihu.com/equation?tex=a%5Cgeq1) 时,
时, ![[公式]](https://www.zhihu.com/equation?tex=ax%5Cgeq+x%5Cgeq+%5Csin+x) ,实数
,实数 ![[公式]](https://www.zhihu.com/equation?tex=a) 的取值范围是
的取值范围是 ![[公式]](https://www.zhihu.com/equation?tex=%5B1%2C%2B%5Cinfty%29) 。
甚至洛必达可以“洛”很多次,只要是不定式就可以“洛”,直到得到结果。
例4 求极限
。
甚至洛必达可以“洛”很多次,只要是不定式就可以“洛”,直到得到结果。
例4 求极限 ![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx%5Crightarrow+0%7D%5Cfrac%7Be%5Ex%2Be%5E%7B-x%7D-2%7D%7Bx%5E2%7D) 。
解答 当
。
解答 当 ![[公式]](https://www.zhihu.com/equation?tex=x%3D+0) 时,
时, ![[公式]](https://www.zhihu.com/equation?tex=e%5Ex%2Be%5E%7B-x%7D-2%3Dx%5E2%3D0) ,使用洛必达法则得:
,使用洛必达法则得:
![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx%5Crightarrow+0%7D%5Cfrac%7Be%5Ex%2Be%5E%7B-x%7D-2%7D%7Bx%5E2%7D%3D%5Clim_%7Bx%5Crightarrow+0%7D%5Cfrac%7Be%5Ex-e%5E%7B-x%7D%7D%7B2x%7D) ,此时依旧得到的是不定式。
当
,此时依旧得到的是不定式。
当 ![[公式]](https://www.zhihu.com/equation?tex=x%3D0) 时,
时, ![[公式]](https://www.zhihu.com/equation?tex=e%5Ex-e%5E%7B-x%7D%3D2x%3D0) ,再次使用洛必达法则得:
,再次使用洛必达法则得:
![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx%5Crightarrow+0%7D%5Cfrac%7Be%5Ex-e%5E%7B-x%7D%7D%7B2x%7D%3D%5Clim_%7Bx%5Crightarrow+0%7D%5Cfrac%7Be%5Ex%2Be%5E%7B-x%7D%7D%7B2%7D%3D1) ,因此
,因此 ![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx%5Crightarrow+0%7D%5Cfrac%7Be%5Ex%2Be%5E%7B-x%7D-2%7D%7Bx%5E2%7D%3D1) 。
。
![[公式]](https://www.zhihu.com/equation?tex=a%5Cgeq+%5Cfrac%7Bf%28x%29%7D%7Bg%28x%29%7D) 的形式,其中
的形式,其中 ![[公式]](https://www.zhihu.com/equation?tex=x) 的临界值是
的临界值是 ![[公式]](https://www.zhihu.com/equation?tex=x_0) ,且
,且 ![[公式]](https://www.zhihu.com/equation?tex=f%28x_0%29%3Dg%28x_0%29%3D0) 。那么很多人就会用洛必达法则,来求出
。那么很多人就会用洛必达法则,来求出 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf%28x%29%7D%7Bg%28x%29%7D) 在
在 ![[公式]](https://www.zhihu.com/equation?tex=x%3Dx_0) 处的极限
处的极限 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf%27%28x_0%29%7D%7Bg%27%28x_0%29%7D) 。但这样做有必要吗?
若
。但这样做有必要吗?
若 ![[公式]](https://www.zhihu.com/equation?tex=g%28x%29%5Cgeq+0) ,则
,则 ![[公式]](https://www.zhihu.com/equation?tex=a%5Cgeq+%5Cfrac%7Bf%28x%29%7D%7Bg%28x%29%7D%5CLeftrightarrow+ag%28x%29-f%28x%29%5Cgeq+0) ,令
,令 ![[公式]](https://www.zhihu.com/equation?tex=%5Cvarphi+%28x%29%3Dag%28x%29-f%28x%29%3D0) ,则原不等式等价于
,则原不等式等价于 ![[公式]](https://www.zhihu.com/equation?tex=%5Cvarphi+%28x%29%5Cgeq+0) 。我们尝试分析构造出来的这个函数。
当
。我们尝试分析构造出来的这个函数。
当 ![[公式]](https://www.zhihu.com/equation?tex=x%3Dx_0) 时,
时, ![[公式]](https://www.zhihu.com/equation?tex=%5Cvarphi+%28x_0%29%3Dag%28x_0%29-f%28x_0%29%3D0) ,一般地,要令我们只要让
,一般地,要令我们只要让 ![[公式]](https://www.zhihu.com/equation?tex=%5Cvarphi+%28x%29) 在
在 ![[公式]](https://www.zhihu.com/equation?tex=x%3Dx_0) 以前单调递减,在
以前单调递减,在 ![[公式]](https://www.zhihu.com/equation?tex=x%3Dx_0) 之后单调递增就行了。
也即
之后单调递增就行了。
也即 ![[公式]](https://www.zhihu.com/equation?tex=x%3Dx_0) 是
是 ![[公式]](https://www.zhihu.com/equation?tex=%5Cvarphi+%28x%29) 的极小值点,令
的极小值点,令 ![[公式]](https://www.zhihu.com/equation?tex=%5Cvarphi+%27%28x_0%29%3Dag%27%28x_0%29-f%27%28x_0%29%3D0) ,可解得
,可解得 ![[公式]](https://www.zhihu.com/equation?tex=a%3D%5Cfrac%7Bf%27%28x_0%29%7D%7Bg%27%28x_0%29%7D) ,这个就和我们用洛必达法则得到的结果一样。
但如果
,这个就和我们用洛必达法则得到的结果一样。
但如果 ![[公式]](https://www.zhihu.com/equation?tex=f%27%28x_0%29%3Dg%27%28x_0%29%3D0) 怎么办呢?可以再求一次导,再令
怎么办呢?可以再求一次导,再令 ![[公式]](https://www.zhihu.com/equation?tex=%5Cvarphi+%27%27%28x_0%29%3Dag%27%27%28x_0%29-f%27%27%28x_0%29%3D0) ,由此解得
,由此解得 ![[公式]](https://www.zhihu.com/equation?tex=a%3D%5Cfrac%7Bf%27%27%28x_0%29%7D%7Bg%27%27%28x_0%29%7D) ,就和多次应用洛必达法则一样。
应评论区要求,补充例题的做法。例如对于刚刚的第二道例题:
例2 当
,就和多次应用洛必达法则一样。
应评论区要求,补充例题的做法。例如对于刚刚的第二道例题:
例2 当 ![[公式]](https://www.zhihu.com/equation?tex=x%3E0) 时,不等式
时,不等式 ![[公式]](https://www.zhihu.com/equation?tex=e%5Ex%5Cgeq+ax%2B1) 恒成立,求实数
恒成立,求实数 ![[公式]](https://www.zhihu.com/equation?tex=a) 的取值范围。
解答 令
的取值范围。
解答 令 ![[公式]](https://www.zhihu.com/equation?tex=f%28x%29%3De%5Ex-ax-1) ,
, ![[公式]](https://www.zhihu.com/equation?tex=x%3E0) ,注意到
,注意到 ![[公式]](https://www.zhihu.com/equation?tex=f%280%29%3D0) 。因此考虑求第一次导。
。因此考虑求第一次导。
![[公式]](https://www.zhihu.com/equation?tex=f%27%28x%29%3De%5Ex-a) ,此时令
,此时令 ![[公式]](https://www.zhihu.com/equation?tex=f%27%280%29%3D1-a%3D0) ,解得
,解得 ![[公式]](https://www.zhihu.com/equation?tex=a%3D1) ,此即为边界值。
由
,此即为边界值。
由 ![[公式]](https://www.zhihu.com/equation?tex=f%27%28x%29) 容易知道
容易知道 ![[公式]](https://www.zhihu.com/equation?tex=f%28x%29) 在
在 ![[公式]](https://www.zhihu.com/equation?tex=%28-%5Cinfty%2C%5Cln+a%29) 单调递减,在
单调递减,在 ![[公式]](https://www.zhihu.com/equation?tex=%28%5Cln+a%2C%2B%5Cinfty%29) 单调递增。
若
单调递增。
若 ![[公式]](https://www.zhihu.com/equation?tex=a%5Cle+1) ,则
,则 ![[公式]](https://www.zhihu.com/equation?tex=%5Cln+a%5Cle+0) ,
, ![[公式]](https://www.zhihu.com/equation?tex=f%28x%29) 在
在 ![[公式]](https://www.zhihu.com/equation?tex=%280%2C%2B%5Cinfty%29) 单调递增,
单调递增, ![[公式]](https://www.zhihu.com/equation?tex=f%28x%29%5Cgeq+f%280%29%3D0) ,满足条件;
若
,满足条件;
若 ![[公式]](https://www.zhihu.com/equation?tex=a%3E1) ,则
,则 ![[公式]](https://www.zhihu.com/equation?tex=f%28x%29) 在
在 ![[公式]](https://www.zhihu.com/equation?tex=%280%2C%5Cln+a%29) 递减,在
递减,在 ![[公式]](https://www.zhihu.com/equation?tex=%28%5Cln+a%2C%2B%5Cinfty%29) 递增,任取
递增,任取 ![[公式]](https://www.zhihu.com/equation?tex=x%5Cin+%280%2C%5Cln+a%29) ,可以推出
,可以推出 ![[公式]](https://www.zhihu.com/equation?tex=f%28x%29%3C+f%280%29%3D0) ,此与
,此与 ![[公式]](https://www.zhihu.com/equation?tex=f%28x%29%5Cgeq+0) 矛盾。
综上,
矛盾。
综上, ![[公式]](https://www.zhihu.com/equation?tex=a) 的取值范围是
的取值范围是 ![[公式]](https://www.zhihu.com/equation?tex=%28-%5Cinfty+%2C1%5D) 。
由此看来,“洛必达法则”完全没有必要出现在题目里,要使用洛必达,其实等价于直接对构造出来的函数求多次导。
在做解答题时,可以先用洛必达法则猜出答案,但是在写过程的时候,还是要用分类讨论的办法,把讨论的过程写清楚。
顺便也提醒高中生,不要盲目寻求一些“秒杀”的办法,最后反而弄巧成拙。
作者:Dylaaan
来源:知乎
。
由此看来,“洛必达法则”完全没有必要出现在题目里,要使用洛必达,其实等价于直接对构造出来的函数求多次导。
在做解答题时,可以先用洛必达法则猜出答案,但是在写过程的时候,还是要用分类讨论的办法,把讨论的过程写清楚。
顺便也提醒高中生,不要盲目寻求一些“秒杀”的办法,最后反而弄巧成拙。
作者:Dylaaan
来源:知乎
二、洛必达法则的小应用
举几个简单的小例子,来说明一下在高中的题目里,洛必达法则怎么用。 例1 画出函数
三、洛必达能不能用?如何绕开洛必达法则?
其实我反复强调的是,高中数学没有极限的定义,上面的过程是不严谨的。 不同的省份改卷标准不一样,有的地方可能会给分,有的地方可能会酌情扣分,而有的地方甚至会一分都不给。 洛必达法则本来是个高等数学中非常有用的结论,但“洛必达”最后变成了一些高中生装逼用的词,遇到题目就“洛”,以为可以秒杀,但完全没有顾及到严谨性。 除此之外,许多高中生在不是不定式的情况下胡乱“洛”,最后得到一个完全错误的答案。结果这些人就开始到处问“为什么这题不能洛必达?”、“洛必达是不是错的?”。 事实上,在做题的过程中,完全可以绕开洛必达法则,达到相同的效果。 一般地说,在遇到恒成立问题时,将不等式进行分离后可以得到形如本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。