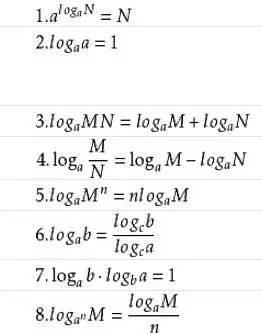 对数函数定义
一般地,函数y=logax(a>0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。
其中x是自变量,函数的定义域是(0,+∞)。它实际上就是指数函数的反函数,可表示为x=ay。因此指数函数里对于a的规定,同样适用于对数函数。
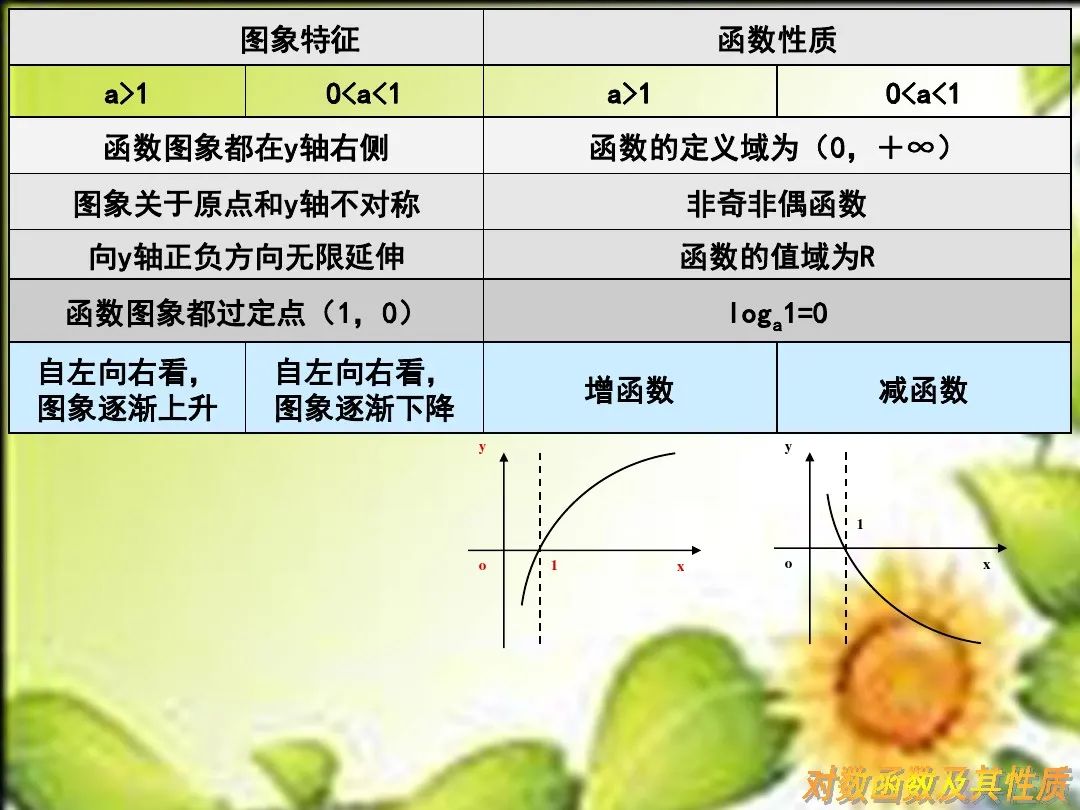
对数函数性质
对数函数定义
一般地,函数y=logax(a>0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。
其中x是自变量,函数的定义域是(0,+∞)。它实际上就是指数函数的反函数,可表示为x=ay。因此指数函数里对于a的规定,同样适用于对数函数。
对数函数性质
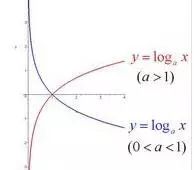 定义域求解:对数函数y=logax的定义域是{x丨x>0},但如果遇到对数型复合函数的定义域的求解,除了要注意大于0以外,还应注意底数大于0且不等于1,如求函数y=logx(2x-1)的定义域,需同时满足x>0且x≠1和2x-1>0,得到x>1/2且x≠1,即其定义域为{x丨x>1/2且x≠1}
值域:实数集R,显然对数函数无界。
定点:函数图像恒过定点(1,0)。
单调性:a>1时,在定义域上为单调增函数;
奇偶性:非奇非偶函数
周期性:不是周期函数
对称性:无
最值:无
零点:x=1
注意:负数和0没有对数。
两句经典话:底真同对数正,底真异对数负。
定义域求解:对数函数y=logax的定义域是{x丨x>0},但如果遇到对数型复合函数的定义域的求解,除了要注意大于0以外,还应注意底数大于0且不等于1,如求函数y=logx(2x-1)的定义域,需同时满足x>0且x≠1和2x-1>0,得到x>1/2且x≠1,即其定义域为{x丨x>1/2且x≠1}
值域:实数集R,显然对数函数无界。
定点:函数图像恒过定点(1,0)。
单调性:a>1时,在定义域上为单调增函数;
奇偶性:非奇非偶函数
周期性:不是周期函数
对称性:无
最值:无
零点:x=1
注意:负数和0没有对数。
两句经典话:底真同对数正,底真异对数负。
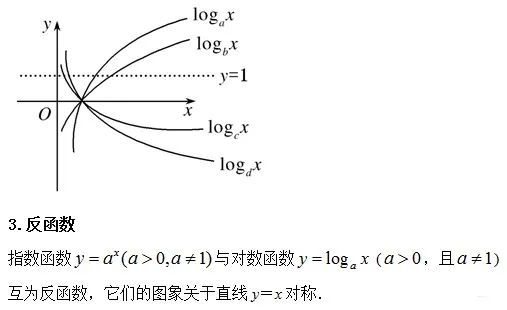
解释如下 也就是说:若y=logab (其中a>0,a≠1,b>0)当a>1,b>1时,y=logab>0; 当0<a<1,b>1时,y=logab<0;</a<1,b> 当a>1,0<b<1时,y=logab<0。< p=""></b<1时,y=logab<0。<>

 教案:
教材分析
本节课在已学对数函数的概念,接着研究对数函数的图像和性质,从而深化学生对对数函数的理解,并且了解较为全面的研究函数的方法,为以后在研究函数增长类型打下基础。另外,我们日常生活中的很多方面都涉及到了对数函数的知识,例如溶液酸碱度的测量,所以学习这一节具有很大的现实价值。
教学目标与核心素养
课程目标
1、掌握对数函数的图象和性质,培养学生实际应用函数的能力;
2、通过观察图象,分析、归纳、总结对数函数的性质;
3、在对数函数的学习过程中,体验数学的科学价值并养成勇于探索的良好习惯.
数学学科素养
1.数学抽象:对数函数的图像与性质;
2.逻辑推理:图像平移问题;
3.数学运算:求函数的定义域与值域;
4.数据分析:利用对数函数的性质比较两个函数值的大小及解对数不等式;
5.数学建模:通过由抽象到具体,由具体到一般的数形结合思想总结指数函数性质.
教学重难点
重点:对数函数的图象和性质;
难点:对底数的分类,如何由图象、解析式归纳对数函数的性质.
课前准备
教学方法:以学生为主体,采用诱思探究式教学,精讲多练。
教学工具:多媒体。
教学过程
一、 情景导入
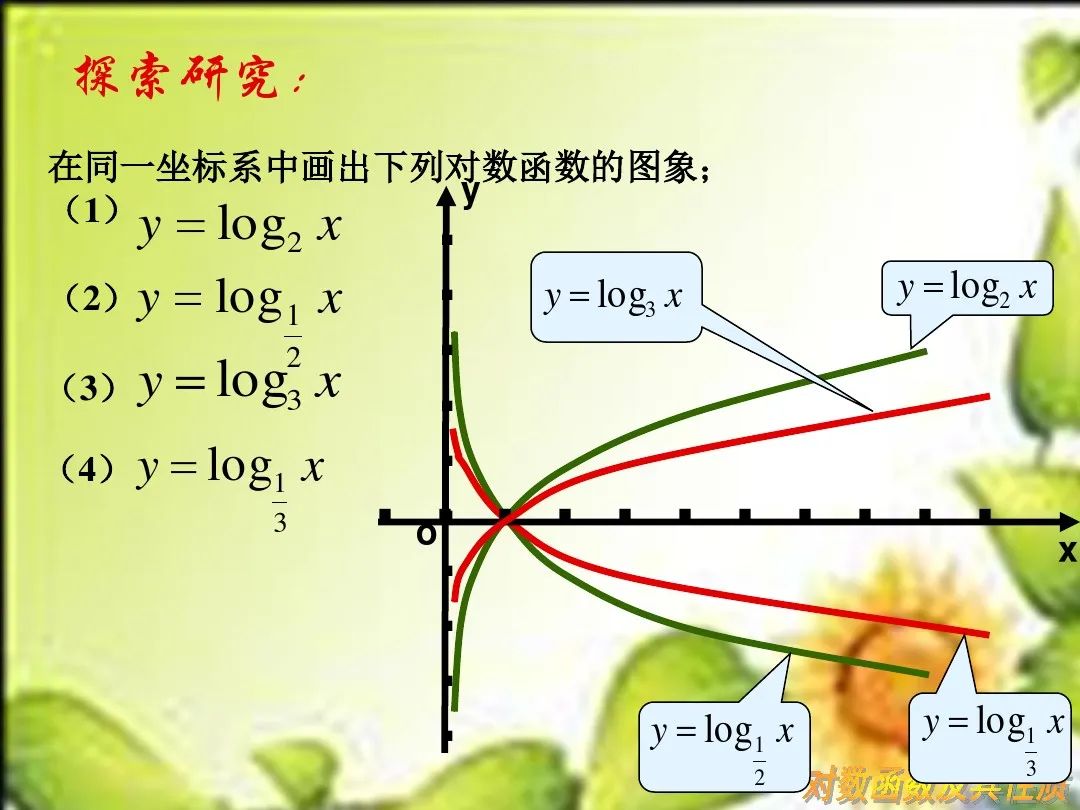
请学生用三点画图法画图像,观察两个函数图像猜测对数函数有哪些性质?
要求:让学生自由发言,教师不做判断。而是引导学生进一步观察.研探.
二、 预习课本,引入新课
阅读课本132-133页,思考并完成以下问题
1. 对数函数的图象是什么,通过图象可观察到对数函数具有哪些性质?
2. 反函数的概念是什么?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
三、 新知探究
1.对数函数的图象及性质
教案:
教材分析
本节课在已学对数函数的概念,接着研究对数函数的图像和性质,从而深化学生对对数函数的理解,并且了解较为全面的研究函数的方法,为以后在研究函数增长类型打下基础。另外,我们日常生活中的很多方面都涉及到了对数函数的知识,例如溶液酸碱度的测量,所以学习这一节具有很大的现实价值。
教学目标与核心素养
课程目标
1、掌握对数函数的图象和性质,培养学生实际应用函数的能力;
2、通过观察图象,分析、归纳、总结对数函数的性质;
3、在对数函数的学习过程中,体验数学的科学价值并养成勇于探索的良好习惯.
数学学科素养
1.数学抽象:对数函数的图像与性质;
2.逻辑推理:图像平移问题;
3.数学运算:求函数的定义域与值域;
4.数据分析:利用对数函数的性质比较两个函数值的大小及解对数不等式;
5.数学建模:通过由抽象到具体,由具体到一般的数形结合思想总结指数函数性质.
教学重难点
重点:对数函数的图象和性质;
难点:对底数的分类,如何由图象、解析式归纳对数函数的性质.
课前准备
教学方法:以学生为主体,采用诱思探究式教学,精讲多练。
教学工具:多媒体。
教学过程
一、 情景导入
请学生用三点画图法画图像,观察两个函数图像猜测对数函数有哪些性质?
要求:让学生自由发言,教师不做判断。而是引导学生进一步观察.研探.
二、 预习课本,引入新课
阅读课本132-133页,思考并完成以下问题
1. 对数函数的图象是什么,通过图象可观察到对数函数具有哪些性质?
2. 反函数的概念是什么?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
三、 新知探究
1.对数函数的图象及性质
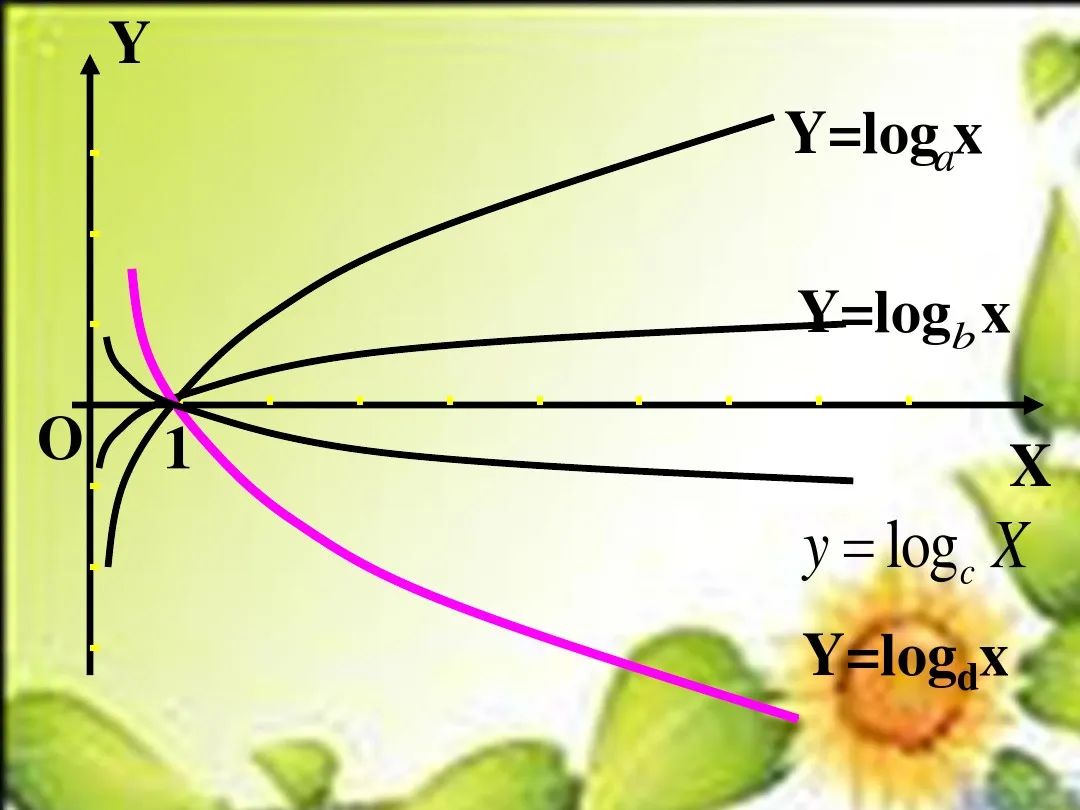
 [点睛] 底数a与1的大小关系决定了对数函数图象的“升降”:当a>1时,对数函数的图象“上升”;当0<a<1时,对数函数的图象“下降”.
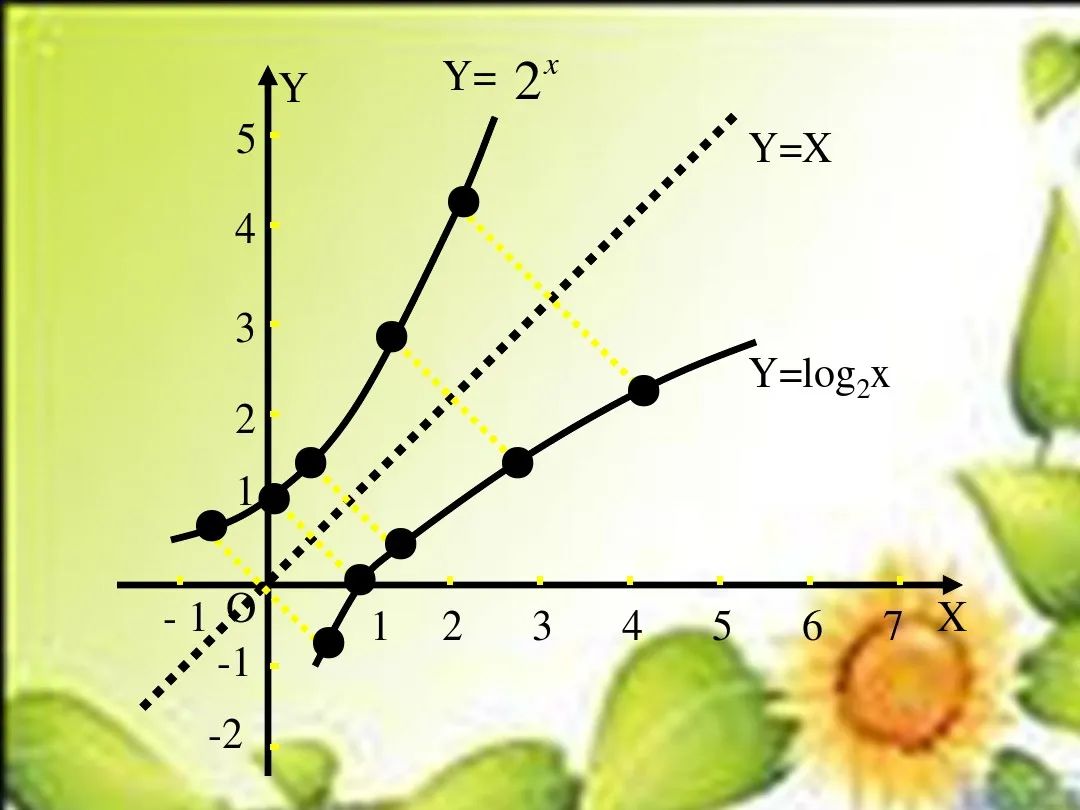
2.反函数
指数函数y=ax和对数函数y=logax(a>0且a≠1)互为反函数.
四、典例分析、举一反三
题型一 对数函数的图象
[点睛] 底数a与1的大小关系决定了对数函数图象的“升降”:当a>1时,对数函数的图象“上升”;当0<a<1时,对数函数的图象“下降”.
2.反函数
指数函数y=ax和对数函数y=logax(a>0且a≠1)互为反函数.
四、典例分析、举一反三
题型一 对数函数的图象
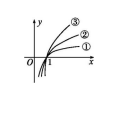
 (3)从(2)的图中你发现了什么?
【答案】见解析
(3)从(2)的图中你发现了什么?
【答案】见解析
 最后把y=lg(x-1)的图象在x轴下方的部分对称翻折到x轴上方(原来在x轴上方的部分不变),即得出函数y=|lg(x-1)|的图象(如图③).
由图易知其定义域为(1,+∞),值域为[0,+∞),单调递减区间为(1,2],单调递增区间为(2,+∞).
题型二 比较对数值的大小
例2 比较下列各组数中两个值的大小:
(1)log23.4,log28.5;
(2)log0.31.8,log0.32.7;
(3)loga5.1,loga5.9(a>0,且a≠1).
【答案】(1) log23.4<log28.5 (2) log0.31.8>log0.32.7 (3)当a>1时,loga5.1<loga5.9;当0<a<1时,loga5.1>loga5.9.
【解析】(1)考察对数函数y=log2x,因为它的底数2>1,所以它在(0,+∞)上是增函数,于是log23.4<log28.5.
(2)考察对数函数y=log0.3x,因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是log0.31.8>log0.32.7.
(3)当a>1时,y=logax在(0,+∞)上是增函数,于是loga5.1<loga5.9;
当0<a<1时,y=logax在(0,+∞)上是减函数,于是loga5.1>loga5.9.
解题技巧:(比较对数值大小时常用的4种方法)
(1)同底的利用对数函数的单调性.
(2) 同真的利用对数函数的图象或用换底公式转化.
(3) 底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨论.
跟踪训练二
1.比较下列各题中两个值的大小:
(1)lg 6,lg 8; (2)log0.56,log0.54;
(3)log2与log2; (4)log23与log54.
【答案】(1)lg 6<lg 8(2)log0.56<log 0.54(3)log2<log2(4)log23>log54.
【解析】(1)因为函数y=lg x在(0,+∞)上是增函数,且6<8,所以lg 6<lg 8.
(2)因为函数y=log0.5x在(0,+∞)上是减函数,且6>4,所以log0.56<log 0.54.
最后把y=lg(x-1)的图象在x轴下方的部分对称翻折到x轴上方(原来在x轴上方的部分不变),即得出函数y=|lg(x-1)|的图象(如图③).
由图易知其定义域为(1,+∞),值域为[0,+∞),单调递减区间为(1,2],单调递增区间为(2,+∞).
题型二 比较对数值的大小
例2 比较下列各组数中两个值的大小:
(1)log23.4,log28.5;
(2)log0.31.8,log0.32.7;
(3)loga5.1,loga5.9(a>0,且a≠1).
【答案】(1) log23.4<log28.5 (2) log0.31.8>log0.32.7 (3)当a>1时,loga5.1<loga5.9;当0<a<1时,loga5.1>loga5.9.
【解析】(1)考察对数函数y=log2x,因为它的底数2>1,所以它在(0,+∞)上是增函数,于是log23.4<log28.5.
(2)考察对数函数y=log0.3x,因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是log0.31.8>log0.32.7.
(3)当a>1时,y=logax在(0,+∞)上是增函数,于是loga5.1<loga5.9;
当0<a<1时,y=logax在(0,+∞)上是减函数,于是loga5.1>loga5.9.
解题技巧:(比较对数值大小时常用的4种方法)
(1)同底的利用对数函数的单调性.
(2) 同真的利用对数函数的图象或用换底公式转化.
(3) 底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨论.
跟踪训练二
1.比较下列各题中两个值的大小:
(1)lg 6,lg 8; (2)log0.56,log0.54;
(3)log2与log2; (4)log23与log54.
【答案】(1)lg 6<lg 8(2)log0.56<log 0.54(3)log2<log2(4)log23>log54.
【解析】(1)因为函数y=lg x在(0,+∞)上是增函数,且6<8,所以lg 6<lg 8.
(2)因为函数y=log0.5x在(0,+∞)上是减函数,且6>4,所以log0.56<log 0.54.
 题型三 比较对数值的大小
题型三 比较对数值的大小
 解题技巧:(常见对数不等式的2种解法)
(1)形如logax>logab的不等式,借助y=logax的单调性求解,如果a的取值不确定,需分a>1与0<a<1两种情况讨论.(2)形如logax>b的不等式,应将b化为以a为底数的对数式的形式,再借助y=logax的单调性求解.
跟踪训练三
1.已知loga(3a-1)恒为正,求a的取值范围.
解题技巧:(常见对数不等式的2种解法)
(1)形如logax>logab的不等式,借助y=logax的单调性求解,如果a的取值不确定,需分a>1与0<a<1两种情况讨论.(2)形如logax>b的不等式,应将b化为以a为底数的对数式的形式,再借助y=logax的单调性求解.
跟踪训练三
1.已知loga(3a-1)恒为正,求a的取值范围.
 题型四 有关对数型函数的值域与最值问题
例4 求下列函数的值域.
(1)y=log2(x2+4);(2)y=log (3+2x-x2).
题型四 有关对数型函数的值域与最值问题
例4 求下列函数的值域.
(1)y=log2(x2+4);(2)y=log (3+2x-x2).
 解题技巧:(对数型函数的值域与最值)
(1)求对数型函数的值域,一般需根据对数函数的单调性及真数的取值范围求解.
(2)求函数的值域时,一定要注意定义域对它的影响,结合函数的单调性求解,当函数中含有参数时,有时需讨论参数的取值.
跟踪训练四
1.已知f(x)=2+log3x,x∈[1,9],求函数y=[f(x)]2+f(x2)的最大值及此时x的值.
【答案】当x=3时,y取得最大值,为13.
【解析】y=[f(x)]2+f(x2)=(2+log3x)2+log3x2+2=(log3x)2+6log3x+6=(log3x+3)2-3.
∵f(x)的定义域为[1,9],
∴y=[f(x)]2+f(x2)中,x必须满足1≤x2≤9,
∴1≤x≤3,∴0≤log3x≤1,∴6≤y≤13.
∴当x=3时,y取得最大值,为13.
五、课堂小结
让学生总结本节课所学主要知识及解题技巧
六、板书设计
解题技巧:(对数型函数的值域与最值)
(1)求对数型函数的值域,一般需根据对数函数的单调性及真数的取值范围求解.
(2)求函数的值域时,一定要注意定义域对它的影响,结合函数的单调性求解,当函数中含有参数时,有时需讨论参数的取值.
跟踪训练四
1.已知f(x)=2+log3x,x∈[1,9],求函数y=[f(x)]2+f(x2)的最大值及此时x的值.
【答案】当x=3时,y取得最大值,为13.
【解析】y=[f(x)]2+f(x2)=(2+log3x)2+log3x2+2=(log3x)2+6log3x+6=(log3x+3)2-3.
∵f(x)的定义域为[1,9],
∴y=[f(x)]2+f(x2)中,x必须满足1≤x2≤9,
∴1≤x≤3,∴0≤log3x≤1,∴6≤y≤13.
∴当x=3时,y取得最大值,为13.
五、课堂小结
让学生总结本节课所学主要知识及解题技巧
六、板书设计
 七、作业
课本140页习题4.4
教学反思
本节通过运用对数函数的图像及应用解决相关问题,侧重用实操,培养学生的逻辑思维能力,提高学生的数学素养.
课件:
七、作业
课本140页习题4.4
教学反思
本节通过运用对数函数的图像及应用解决相关问题,侧重用实操,培养学生的逻辑思维能力,提高学生的数学素养.
课件:
















 练习:
1、 函数f(x)对于任意实数x满足条件f(x+4)=
练习:
1、 函数f(x)对于任意实数x满足条件f(x+4)=本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。

 丘成桐:作为家长,如何启蒙和培养孩子对数学的兴趣?
丘成桐:作为家长,如何启蒙和培养孩子对数学的兴趣? 许兴华初中数学竞赛第7讲:指数与对数
许兴华初中数学竞赛第7讲:指数与对数 许兴华初中数学竞赛第8讲:对数杂题
许兴华初中数学竞赛第8讲:对数杂题 对数均值不等式在高考及数学竞赛中的运用
对数均值不等式在高考及数学竞赛中的运用 对数:所有天文学家都应该感谢的数学发现
对数:所有天文学家都应该感谢的数学发现 高考数学解题:对数平均基本不等式(对数均值不等式)
高考数学解题:对数平均基本不等式(对数均值不等式) 对数是怎么被发明的?有两个人都是对数先驱
对数是怎么被发明的?有两个人都是对数先驱 为什么会有自然对数?奈皮尔可没有听说过数字e
为什么会有自然对数?奈皮尔可没有听说过数字e