我教过的许多学生,学了蛮多年数学的同学,少有能够知道如何进行系统尝试进行解题。所以更多时候解题感觉像灵感一样,有时候看了能做,有时候等了许久还是不出来。之前写了关于如何解题的系统思维方法,不过只懂得方法而不执行是远远不够的。
所以,以中考压轴题为题材,以理论结合实践进行介绍,希望大家能在自己的解题过程中刻意训练自己的思维。总得来说:
1、分析题目,列出已知条件,及其你能想到的相关知识点(训练知识点连接,后期对知识熟悉了可以不用手动列出);确定、理解未知因素,要求解或求证的目标。
2、通过思维发散(试错)和逆向搜索两种方式寻找已知到未知目标的路径。在这个过程中可以大胆猜想,小心求证;甚至可以通过去掉一些苛刻的条件或考虑一些特殊的情况,简化问题进行路径探索,分析、确定一条可行路径之后在进行有条有理的解答。
3、在平时的练习中,需要复盘解题路径的步骤,以及花一些时间从不同维度去寻找看是否有其他的路径,找出最优路径。这样知识点的连接得以最大程度加强,且能够提升解答效率。
 接下来,我将通过“中考加油站”分享解题的系统思维训练方法,一方面分享训练方法的关键;另一方面,希望帮助大家建立自己的知识联系。
接下来,我将通过“中考加油站”分享解题的系统思维训练方法,一方面分享训练方法的关键;另一方面,希望帮助大家建立自己的知识联系。
 读完这个问题,你可以先尝试按照这个思维过程自己试一试。
第一步:分析已知条件,列出相关知识点或推导的相关结论,明确求解问题/目标。
抛物线
读完这个问题,你可以先尝试按照这个思维过程自己试一试。
第一步:分析已知条件,列出相关知识点或推导的相关结论,明确求解问题/目标。
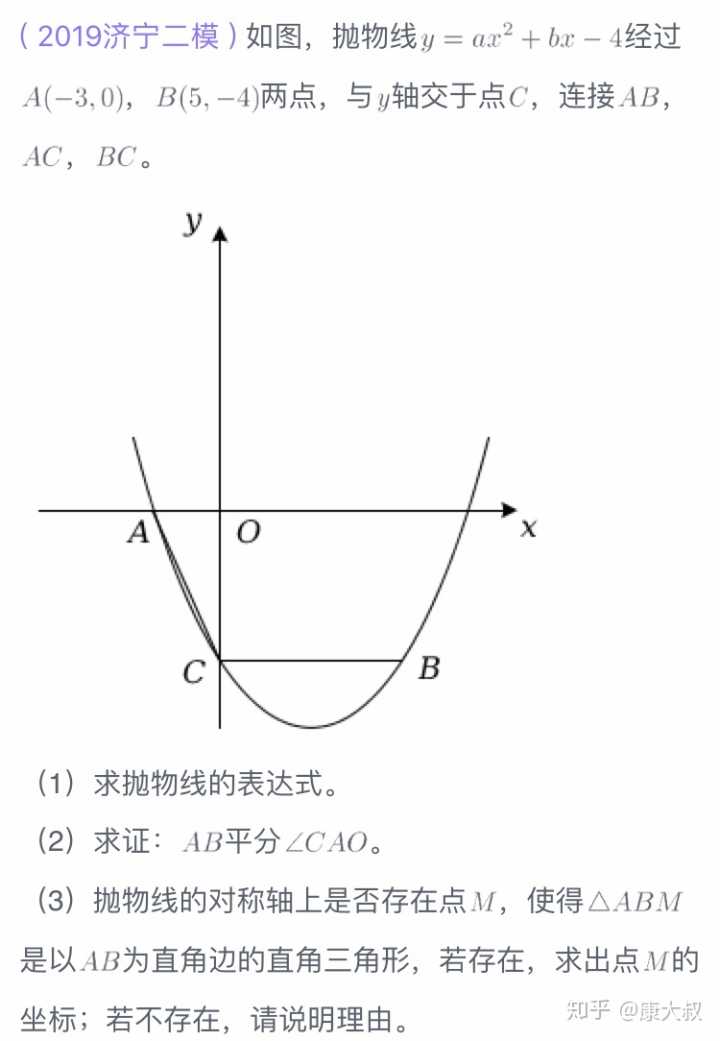
抛物线 ![[公式]](https://www.zhihu.com/equation?tex=y%3Dax%5E%7B2%7D%2Bbx-4) 过两个确定的点A(-3,0),B(5,-4),大部分同学能都反应出来,这个二次函数是一个确定的二次函数,通过代入法,解一个方程组,能够确定二次函数的表达式:
过两个确定的点A(-3,0),B(5,-4),大部分同学能都反应出来,这个二次函数是一个确定的二次函数,通过代入法,解一个方程组,能够确定二次函数的表达式:
![[公式]](https://www.zhihu.com/equation?tex=y%3D%5Cfrac%7B1%7D%7B6%7Dx%5E%7B2%7D-%5Cfrac%7B5%7D%7B6%7Dx-4) 这种问题第一个问题就是送分的,这种问题第一个如果计算错了,后面的计算基本上没戏了,都会错。
所以不要忘记检验一下,将点A带入进行检验:
这种问题第一个问题就是送分的,这种问题第一个如果计算错了,后面的计算基本上没戏了,都会错。
所以不要忘记检验一下,将点A带入进行检验:
![[公式]](https://www.zhihu.com/equation?tex=0%3D%5Cfrac%7B1%7D%7B6%7D%5Ctimes%28-3%29%5E%7B2%7D-%5Cfrac%7B5%7D%7B6%7D%5Ctimes%28-3%29-4%3D%5Cfrac%7B9%7D%7B6%7D%2B%5Cfrac%7B15%7D%7B6%7D-4%3D%5Cfrac%7B24%7D%7B6%7D-4) 是正确的,如果还不放心,可以在将另外一点B带入检验。
很多人都能做,但是得不了分,最主要的原因就是自己解题习惯和专注力不好,还没有检验的习惯。
看第二个问题,然后关于这个问题列出已知条件及其相关知识点,第2个问题是一个平面几何问题,要证明:线段AB平分
是正确的,如果还不放心,可以在将另外一点B带入检验。
很多人都能做,但是得不了分,最主要的原因就是自己解题习惯和专注力不好,还没有检验的习惯。
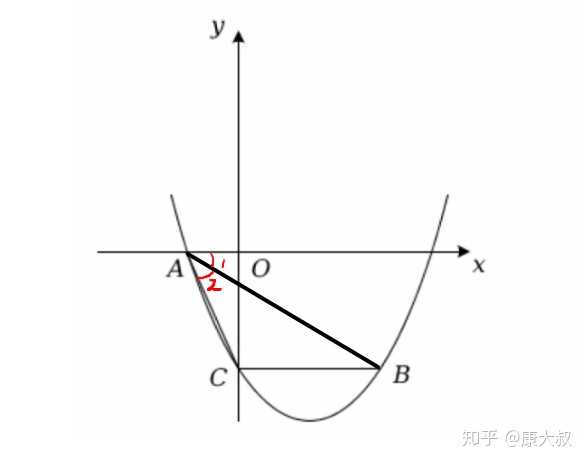
看第二个问题,然后关于这个问题列出已知条件及其相关知识点,第2个问题是一个平面几何问题,要证明:线段AB平分 ![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) CAO,也就是下图中的
CAO,也就是下图中的![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 1=
1=![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 2(角平分线的定义):
2(角平分线的定义):
 我们已经知道什么条件?
通过二次函数解析式确定,我们能够确定的二次函数与X轴和Y轴的交点全部是确定的,求得点C坐标为(0,-4)。因为点B(5,-4),如果你从坐标不能察觉BC平行X轴的话?那么你得从图形大胆猜测是否平行,在进行求证。对称轴
我们已经知道什么条件?
通过二次函数解析式确定,我们能够确定的二次函数与X轴和Y轴的交点全部是确定的,求得点C坐标为(0,-4)。因为点B(5,-4),如果你从坐标不能察觉BC平行X轴的话?那么你得从图形大胆猜测是否平行,在进行求证。对称轴 ![[公式]](https://www.zhihu.com/equation?tex=x_%7B0%7D%3D-%5Cfrac%7Bb%7D%7B2a%7D%3D%5Cfrac%7B5%7D%7B2%7D) ,也是确定的,但目前这个问题用不到,韦达定理也用不到,不过这些知识点属于二次函数最基础的知识点了,需要大脑能够随时召唤出来。
第二步:逆向搜索法寻找路径
对于证明题比较容易的一种方式,就是假设这个结论成立
,也是确定的,但目前这个问题用不到,韦达定理也用不到,不过这些知识点属于二次函数最基础的知识点了,需要大脑能够随时召唤出来。
第二步:逆向搜索法寻找路径
对于证明题比较容易的一种方式,就是假设这个结论成立![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 1=
1=![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 2。然后看上面面这个图,你能得出哪些结论?这个就是我说的“逆向搜索”。
假设
2。然后看上面面这个图,你能得出哪些结论?这个就是我说的“逆向搜索”。
假设![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 1=
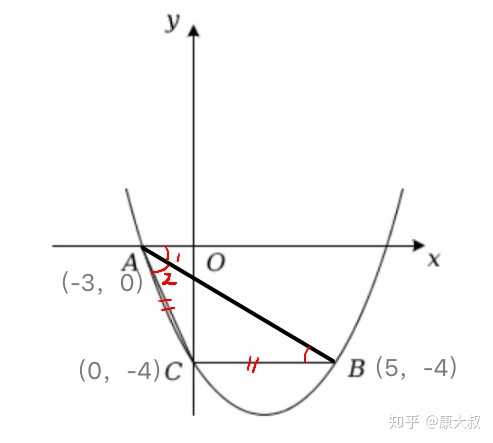
1=![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 2。看这个下面图形,因为点C(0,-4)与点B(5,-4),他们纵坐标相同都为-4,所以
2。看这个下面图形,因为点C(0,-4)与点B(5,-4),他们纵坐标相同都为-4,所以 ![[公式]](https://www.zhihu.com/equation?tex=L_%7BBC%7D) (表示线段BC所在的直线):
(表示线段BC所在的直线): ![[公式]](https://www.zhihu.com/equation?tex=y%3D-4) 与Y轴垂直,即
与Y轴垂直,即![[公式]](https://www.zhihu.com/equation?tex=L_%7BBC%7D) //X轴
//X轴 ![[公式]](https://www.zhihu.com/equation?tex=%5CLeftrightarrow)
![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 1=
1=![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) B(两直线平行,内错角相等;平行线判定定理)也就是说在假设
B(两直线平行,内错角相等;平行线判定定理)也就是说在假设![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 1=
1=![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 2时,得到
2时,得到![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 2=
2=![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) B相等,
B相等, ![[公式]](https://www.zhihu.com/equation?tex=%5Ctriangle) ABC是等腰三角形。
ABC是等腰三角形。
 所以反过来,只需要证明,
所以反过来,只需要证明, ![[公式]](https://www.zhihu.com/equation?tex=%5Ctriangle) ABC是等腰三角形,就能得到我们的结论:
ABC是等腰三角形,就能得到我们的结论:![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 1=
1=![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 2,即线段AB平分
2,即线段AB平分 ![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) CAO。
因为点A、B、C都是确定的,所以根据任意两点的距离公式可以求得两点的距离。
两点
CAO。
因为点A、B、C都是确定的,所以根据任意两点的距离公式可以求得两点的距离。
两点 ![[公式]](https://www.zhihu.com/equation?tex=A%28x_%7BA%7D%2Cy_%7BA%7D%29%E3%80%81B%EF%BC%88x_%7BB%7D%2Cy_%7BB%7D%EF%BC%89) 的距离公式:
的距离公式:![[公式]](https://www.zhihu.com/equation?tex=%7CAB%7C%3D%5Csqrt%7B%EF%BC%88x_%7BA%7D-x_%7BB%7D%29%5E2%2B%28y_%7BA%7D-x_%7BB%7D%29%5E2%7D) (可由勾股定理推导)。
而这里AC、BC的长度比较特别,AC使用勾股定理求得,BC使用横坐标相减得到。
因为要证明的结论一定是正确的,所以由结论推出的相关结论也一定是正确的。这样我们就通过“逆向搜索”的方法找到一条可行的路径。
从正向来看:
(1)由计算|AC|与|BC|的长度
(可由勾股定理推导)。
而这里AC、BC的长度比较特别,AC使用勾股定理求得,BC使用横坐标相减得到。
因为要证明的结论一定是正确的,所以由结论推出的相关结论也一定是正确的。这样我们就通过“逆向搜索”的方法找到一条可行的路径。
从正向来看:
(1)由计算|AC|与|BC|的长度 ![[公式]](https://www.zhihu.com/equation?tex=%5CRightarrow%5Cleft%7C+AC+%5Cright%7C%3D%5Cleft%7C+BC+%5Cright%7C) ,证明
,证明![[公式]](https://www.zhihu.com/equation?tex=%5Ctriangle) ABC是等腰三角形
ABC是等腰三角形 ![[公式]](https://www.zhihu.com/equation?tex=%5CRightarrow)
![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 2=
2=![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) B。(等腰三角形的定义)
(2)
B。(等腰三角形的定义)
(2)![[公式]](https://www.zhihu.com/equation?tex=L_%7BBC%7D) //X轴
//X轴![[公式]](https://www.zhihu.com/equation?tex=%5CRightarrow)
![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 1=
1=![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) B。(平行线的性质)
(3)综上两步,求证结论:1=
B。(平行线的性质)
(3)综上两步,求证结论:1=![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 2,即线段AB平分
2,即线段AB平分 ![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) CAO。
第三步:从其他维度再看看,是否有其他路径,比较不同路径寻找最优:
我们通过二次函数确定,我们得到知道:
CAO。
第三步:从其他维度再看看,是否有其他路径,比较不同路径寻找最优:
我们通过二次函数确定,我们得到知道:![[公式]](https://www.zhihu.com/equation?tex=L_%7BBC%7D) //X轴,因为要证明角度相等关系,1=
//X轴,因为要证明角度相等关系,1=![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) 2,其实就是把
2,其实就是把![[公式]](https://www.zhihu.com/equation?tex=%5Ctriangle) ABC按照直线AB对折,且点C一定落到X轴上。
所以在平面图形中,有哪些平面图形能够对折成三角形呢?
肯定是一个四边形,正方形可以,平行四边形是否也可以?只是平行四边形肯定不行,但是边相等的平行四边形——菱形则可以,长方形也不行。
ABC按照直线AB对折,且点C一定落到X轴上。
所以在平面图形中,有哪些平面图形能够对折成三角形呢?
肯定是一个四边形,正方形可以,平行四边形是否也可以?只是平行四边形肯定不行,但是边相等的平行四边形——菱形则可以,长方形也不行。
![[公式]](https://www.zhihu.com/equation?tex=%5Cangle) CAO明显不等于90度,所以只有菱形了。这个时候我们就可以构造一个菱形,也就是邻边相等(即四边相等)的平行四边形。
所以这个时候我们才会想到去计算|AC|与|BC|的长度
CAO明显不等于90度,所以只有菱形了。这个时候我们就可以构造一个菱形,也就是邻边相等(即四边相等)的平行四边形。
所以这个时候我们才会想到去计算|AC|与|BC|的长度 ![[公式]](https://www.zhihu.com/equation?tex=%5CRightarrow%5Cleft%7C+AC+%5Cright%7C%3D%5Cleft%7C+BC+%5Cright%7C) 。
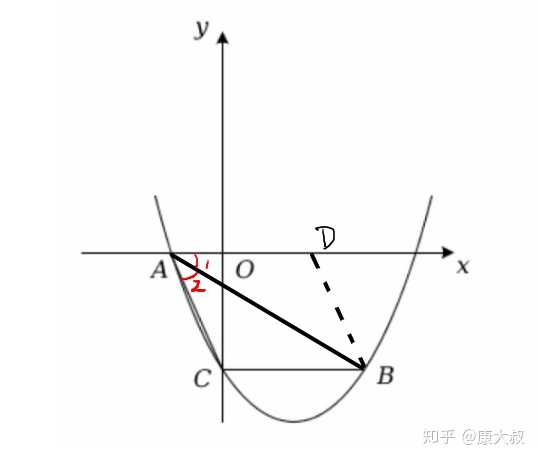
要构造平行四边形,则过点B做平行于AC的线段交X轴于点D,四边形ABCD是平行四边形,且邻边相等,所以也是菱形。用菱形的性质:对角线平分对角也就证明了结论。
复盘下步骤:
(1)做平行与AC的线段BD,结合BC平行X轴,得到平行四边形ABCD;
(2)计算|AC|与|BC|的长度
。
要构造平行四边形,则过点B做平行于AC的线段交X轴于点D,四边形ABCD是平行四边形,且邻边相等,所以也是菱形。用菱形的性质:对角线平分对角也就证明了结论。
复盘下步骤:
(1)做平行与AC的线段BD,结合BC平行X轴,得到平行四边形ABCD;
(2)计算|AC|与|BC|的长度 ![[公式]](https://www.zhihu.com/equation?tex=%5CRightarrow%5Cleft%7C+AC+%5Cright%7C%3D%5Cleft%7C+BC+%5Cright%7C) ,得到四边形ABCD是菱形;
(3)由菱形的性质,角平分线平分内角,结论得证。
这两种解题路径通过逆向分析,只是看待的维度不同,进一步引导我们去寻找达成目标的条件,所涉及的知识点是不同的,路径1是用到了平行线性质和等腰三角形的概念,等式的传递性;路径2则是构造了菱形,应用菱形本身的性质。但其实这些知识都具有一定的相关性:
菱形关于对角线对称,是邻边相等的平行四边形,且由两个等腰三角形组成,还能想到对角线平分对角,形成4组相等的角,且两条对角线的交点是对角线的中点,对角线垂直等。
这样我们对这些相关知识点的联系都得到了进一步的加强稳固。
,得到四边形ABCD是菱形;
(3)由菱形的性质,角平分线平分内角,结论得证。
这两种解题路径通过逆向分析,只是看待的维度不同,进一步引导我们去寻找达成目标的条件,所涉及的知识点是不同的,路径1是用到了平行线性质和等腰三角形的概念,等式的传递性;路径2则是构造了菱形,应用菱形本身的性质。但其实这些知识都具有一定的相关性:
菱形关于对角线对称,是邻边相等的平行四边形,且由两个等腰三角形组成,还能想到对角线平分对角,形成4组相等的角,且两条对角线的交点是对角线的中点,对角线垂直等。
这样我们对这些相关知识点的联系都得到了进一步的加强稳固。
 第三问,就用到了二次函数的对称轴,要在对称轴上找一个点M,使得三角形ABM是直角三角形,并且AB是直角边,也就是说点A是垂点或者点B是垂点,即
第三问,就用到了二次函数的对称轴,要在对称轴上找一个点M,使得三角形ABM是直角三角形,并且AB是直角边,也就是说点A是垂点或者点B是垂点,即 ![[公式]](https://www.zhihu.com/equation?tex=MA%5Cbot+AB) 或
或 ![[公式]](https://www.zhihu.com/equation?tex=MB%5Cbot+AB) 。问是否存在,存在要求出坐标,不存在要说明理由。
。问是否存在,存在要求出坐标,不存在要说明理由。
 同样分析一下,已知条件是点M在对称轴上,所以M的坐标(
同样分析一下,已知条件是点M在对称轴上,所以M的坐标( ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B5%7D%7B2%7D) ,m)表示。我们可以先想像一下,当点M从X轴(点F)向上面无穷远处移动时,直线AM会逼近垂直X轴的直线
,m)表示。我们可以先想像一下,当点M从X轴(点F)向上面无穷远处移动时,直线AM会逼近垂直X轴的直线 ![[公式]](https://www.zhihu.com/equation?tex=L_%7BA%7D) ,
, ![[公式]](https://www.zhihu.com/equation?tex=%5Cangle+MAB) 逼近一个钝角,所以反过来,当点M从无穷远向下移动,靠近X轴点F的过程,一定有一个点M使得
逼近一个钝角,所以反过来,当点M从无穷远向下移动,靠近X轴点F的过程,一定有一个点M使得![[公式]](https://www.zhihu.com/equation?tex=MA%5Cbot+AB) 。
同理在点F下方移动到负无穷远时,一定也有一个点M使得得
。
同理在点F下方移动到负无穷远时,一定也有一个点M使得得![[公式]](https://www.zhihu.com/equation?tex=MB%5Cbot+AB) 。请想一想为什么不是
。请想一想为什么不是![[公式]](https://www.zhihu.com/equation?tex=MA%5Cbot+AB) ?
因为就算点M在X轴下面不论多远,MA所在直线逼近
?
因为就算点M在X轴下面不论多远,MA所在直线逼近![[公式]](https://www.zhihu.com/equation?tex=L_%7BA%7D) ,
,![[公式]](https://www.zhihu.com/equation?tex=%5Cangle+MAB) 逼近一个锐角,所以是不可能垂直于A点。同理M点在X轴上方时,也不能垂直于B点。
当然这些分析在大脑中进行就好了,不用写在解题过程中,但动点问题,移动的这个过程思维非常重要,能够让我们对问题理解更加深刻。
对于这类是否存在的题。可以类似看成求证题,假设存在,得到一个条件,与其他已知条件进行求解,能够求解出来,则存在,求解不出来,可以说不存在。当然前提是你的方法是正确的。
逼近一个锐角,所以是不可能垂直于A点。同理M点在X轴上方时,也不能垂直于B点。
当然这些分析在大脑中进行就好了,不用写在解题过程中,但动点问题,移动的这个过程思维非常重要,能够让我们对问题理解更加深刻。
对于这类是否存在的题。可以类似看成求证题,假设存在,得到一个条件,与其他已知条件进行求解,能够求解出来,则存在,求解不出来,可以说不存在。当然前提是你的方法是正确的。
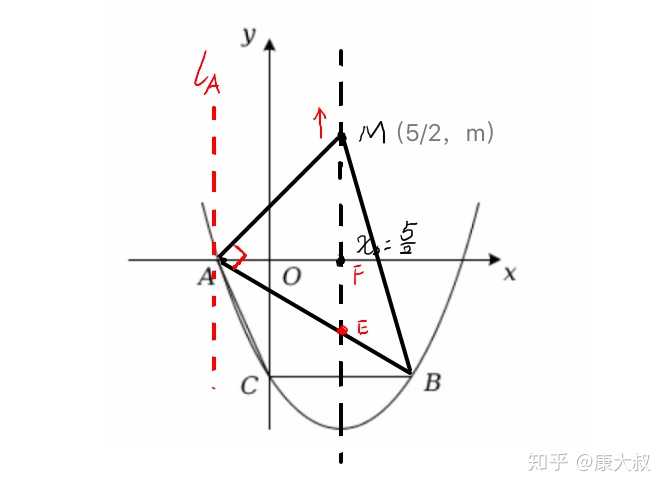 所以,通过我们的分析,存在两种情况,这里我主要分析在X轴上方的情况。大家可以考虑在下方的情况如何快速求解。因为点M横坐标是知道的,只需要求纵坐标m即可,也就是上面MF的长度。
我们看到在三角形ABM中有很多直角三角形,例如
所以,通过我们的分析,存在两种情况,这里我主要分析在X轴上方的情况。大家可以考虑在下方的情况如何快速求解。因为点M横坐标是知道的,只需要求纵坐标m即可,也就是上面MF的长度。
我们看到在三角形ABM中有很多直角三角形,例如 ![[公式]](https://www.zhihu.com/equation?tex=Rt%5Ctriangle+AME%E3%80%81Rt%5Ctriangle+AMF%E3%80%81Rt%5Ctriangle+AFE) 。这个时候可以同相似三角形进行求解,当然如果你熟悉射影定理,也可以直接使用:
。这个时候可以同相似三角形进行求解,当然如果你熟悉射影定理,也可以直接使用:
![[公式]](https://www.zhihu.com/equation?tex=%7CAF%7C%5E%7B2%7D%3D%7CMF%7C%C2%B7%7CEF%7C) 点A是确定的,点E也是确定的,用(
点A是确定的,点E也是确定的,用( ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B5%7D%7B2%7D) ,e)表示,并且点E在直线AB上,通过定点A(-3,0)、B(-4,5)使用待定系数法
,e)表示,并且点E在直线AB上,通过定点A(-3,0)、B(-4,5)使用待定系数法 ![[公式]](https://www.zhihu.com/equation?tex=L_%7BAB%7D%EF%BC%9Ay%3Dkx%2Bb) 求出直线AB的表达式
求出直线AB的表达式![[公式]](https://www.zhihu.com/equation?tex=L_%7BAB%7D%EF%BC%9Ay%3D-5x-15) ,点E(
,点E( ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B5%7D%7B2%7D) ,e)在直线AB上,在就能得出e=
,e)在直线AB上,在就能得出e=![[公式]](https://www.zhihu.com/equation?tex=-%5Cfrac%7B55%7D%7B2%7D) 。
。
![[公式]](https://www.zhihu.com/equation?tex=%7CAF%7C%5E%7B2%7D%3D%7CMF%7C%C2%B7%7CEF%7C%5CLeftrightarrow++%5B%5Cfrac%7B5%7D%7B2%7D-%EF%BC%88-3%EF%BC%89%5D%5E%7B2%7D%3Dm%C2%B7%7Ce%7C%3Dm%C2%B7%5Cfrac%7B55%7D%7B2%7D%5CRightarrow+m%3D%5Cfrac%7B11%7D%7B10%7D) 。
所以在X轴上方,存在点M
。
所以在X轴上方,存在点M ![[公式]](https://www.zhihu.com/equation?tex=%EF%BC%88%5Cfrac%7B5%7D%7B2%7D%EF%BC%8C%5Cfrac%7B11%7D%7B10%7D%EF%BC%89) 。
这是利用平面几何中相似三角形推导出来的射影定理进行求解,如果你不知道这个定理。也同样可以使用两个相似三角形线段成比例同样可以求解:
。
这是利用平面几何中相似三角形推导出来的射影定理进行求解,如果你不知道这个定理。也同样可以使用两个相似三角形线段成比例同样可以求解:
![[公式]](https://www.zhihu.com/equation?tex=%5Ctriangle+AMF+%5Csim+%5Ctriangle+EAF+%5CRightarrow+%5Cfrac%7B%7CAF%7C%7D%7B%7CMF%7C%7D%3D%5Cfrac%7B%7CEF%7C%7D%7B%7CAF%7C%7D+%5CRightarrow+%7CAF%7C%5E%7B2%7D%3D%7CMF%7C%C2%B7%7CEF%7C) (相似三角形对应线段成比例也可以推导出射影定理。)
另外,从纯代数的解析几何方式来看,利用勾股定理,将点M、A、B的坐标带入两点距离公式,也同样可以求解出来:
(相似三角形对应线段成比例也可以推导出射影定理。)
另外,从纯代数的解析几何方式来看,利用勾股定理,将点M、A、B的坐标带入两点距离公式,也同样可以求解出来:
![[公式]](https://www.zhihu.com/equation?tex=%7CMA%7C%5E%7B2%7D%2B%7CAB%7C%5E%7B2%7D+%3D%7CMB%7C%5E%7B2%7D++) ,注意点M的取值,m>0。
,注意点M的取值,m>0。
![[公式]](https://www.zhihu.com/equation?tex=%7CMA%7C%5E2%3D%7B%5B%5Cfrac%7B5%7D%7B2%7D-%EF%BC%88-3%EF%BC%89%5D%5E%7B2%7D%2B%28m-0%29%5E2%7D) 同理,用两点距离公司,可以求出
同理,用两点距离公司,可以求出 ![[公式]](https://www.zhihu.com/equation?tex=%7CAB%7C%5E%7B2%7D) 和
和 ![[公式]](https://www.zhihu.com/equation?tex=%7CMB%7C%5E%7B2%7D++) ,进而通过等式求出m。
综上,我们也找到了第3个问题的两种路径:
通过假设存在。
第一:利用存在的条件和已知点的坐标,通过相似三角形或射影定理,分别求出点M在X轴在上方和下方时的坐标。
第二:通过勾股定理和两点的距离公式建立等量关系进行求解。
第一种是平面几何的相关知识,第二种是解析几何的解法。对于熟悉射影定理的同学来说,通过第一种较为高效。
所以,通常在解题的过程中,要可以去训练自己这样的系统思考过程。这样不论是初中学习还是高中学习,都能够做到从容不迫。
纸上得来终觉浅,绝知此事要躬行。
,进而通过等式求出m。
综上,我们也找到了第3个问题的两种路径:
通过假设存在。
第一:利用存在的条件和已知点的坐标,通过相似三角形或射影定理,分别求出点M在X轴在上方和下方时的坐标。
第二:通过勾股定理和两点的距离公式建立等量关系进行求解。
第一种是平面几何的相关知识,第二种是解析几何的解法。对于熟悉射影定理的同学来说,通过第一种较为高效。
所以,通常在解题的过程中,要可以去训练自己这样的系统思考过程。这样不论是初中学习还是高中学习,都能够做到从容不迫。
纸上得来终觉浅,绝知此事要躬行。
本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。
 接下来,我将通过“中考加油站”分享解题的系统思维训练方法,一方面分享训练方法的关键;另一方面,希望帮助大家建立自己的知识联系。
接下来,我将通过“中考加油站”分享解题的系统思维训练方法,一方面分享训练方法的关键;另一方面,希望帮助大家建立自己的知识联系。








 接下来,我将通过“中考加油站”分享解题的系统思维训练方法,一方面分享训练方法的关键;另一方面,希望帮助大家建立自己的知识联系。
接下来,我将通过“中考加油站”分享解题的系统思维训练方法,一方面分享训练方法的关键;另一方面,希望帮助大家建立自己的知识联系。





