和所有的数学分支类似,概率论的也是经历了从直觉到严格的过程。其中的一个转折点就是贝特朗悖论。
1 古典派
古典派也就是高中时候学的概率论。它的核心哲学思想是:不充分理由原则。
1.1 不充分理由原则
雅各布·伯努利(1654-1705):
 提出,如果因为无知,使得我们没有办法判断哪一个结果会比另外一个结果更容易出现,那么应该给予它们相同的概率。比如:
提出,如果因为无知,使得我们没有办法判断哪一个结果会比另外一个结果更容易出现,那么应该给予它们相同的概率。比如:
- 硬币:由于不清楚硬币哪一面更容易出现,那么应该给予正面、反面相同的概率,即为
![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B1%7D%7B2%7D)
- 骰子:我们不清楚骰子哪一面更容易出现,那么应该给予每一面相同的概率,即为
![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B1%7D%7B6%7D)
此称为 不充分理由原则(Insufficient Reason Principle)。
1.2 古典概率
以不充分理由原则为基础,经由皮埃尔-西蒙·拉普拉斯侯爵(1749-1827):
 之手,确立了 古典概率 的定义,即:
之手,确立了 古典概率 的定义,即:
![[公式]](https://www.zhihu.com/equation?tex=%E6%9C%AA%E7%9F%A5%E7%9A%84%E6%A6%82%E7%8E%87%E9%83%BD%E4%B8%BA%E7%AD%89%E6%A6%82%E7%8E%87%5C%5C) 整个19世纪的人们都广泛接受这个定义,并发展出了一系列的定义和定理。
2 贝特朗悖论
法国数学家贝特朗(也翻译为“伯特兰”)于1888年在他的著作《Calcul des probabilités》中提到了这个悖论:
整个19世纪的人们都广泛接受这个定义,并发展出了一系列的定义和定理。
2 贝特朗悖论
法国数学家贝特朗(也翻译为“伯特兰”)于1888年在他的著作《Calcul des probabilités》中提到了这个悖论:
 原始的悖论比较复杂,下面我们给出一个等价的形式。
2.1 锯木厂的木头
问:有一家锯木厂,它会把木头切成不同的木方,木方的截面都是正方形,边长会在
原始的悖论比较复杂,下面我们给出一个等价的形式。
2.1 锯木厂的木头
问:有一家锯木厂,它会把木头切成不同的木方,木方的截面都是正方形,边长会在![[公式]](https://www.zhihu.com/equation?tex=1%5Csim+3) 尺之间随机浮动:
尺之间随机浮动:
 那么根据古典概率,该锯木厂生产出来的正方形边长在
那么根据古典概率,该锯木厂生产出来的正方形边长在![[公式]](https://www.zhihu.com/equation?tex=1%5Csim+2) 尺之间的概率为多少?
解:根据不充分理由原则,因为不知道哪一种边长更容易出现,那么就应该给予它们相同的概率,也就是说
尺之间的概率为多少?
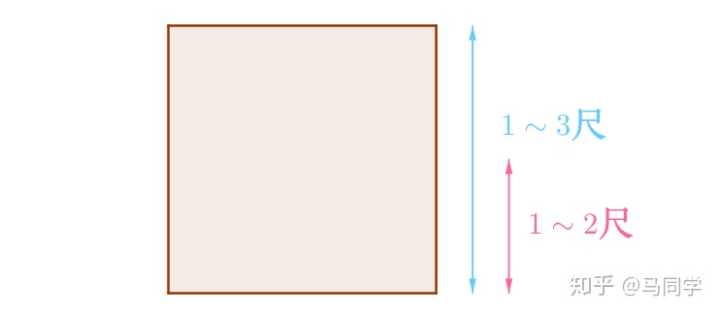
解:根据不充分理由原则,因为不知道哪一种边长更容易出现,那么就应该给予它们相同的概率,也就是说![[公式]](https://www.zhihu.com/equation?tex=1%5Csim+3) 之间每一种长度都是等可能的。而
之间每一种长度都是等可能的。而![[公式]](https://www.zhihu.com/equation?tex=1%5Csim+2) 包含了一半的可能长度:
包含了一半的可能长度:
 所以,正方形边长在
所以,正方形边长在![[公式]](https://www.zhihu.com/equation?tex=1%5Csim+2) 尺之间的概率为:
尺之间的概率为:
![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B2-1%7D%7B3-1%7D%3D%5Cfrac%7B1%7D%7B2%7D%5C%5C) 2.2 悖论的产生
刚才的问题还可以转为面积来解答,
2.2 悖论的产生
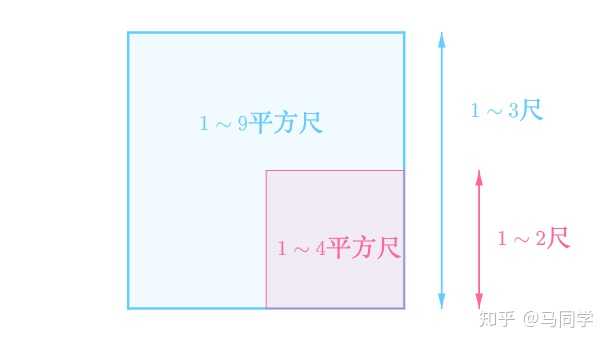
刚才的问题还可以转为面积来解答,![[公式]](https://www.zhihu.com/equation?tex=1%5Csim+3) 尺边长的正方形面积为
尺边长的正方形面积为![[公式]](https://www.zhihu.com/equation?tex=1%5Csim+9) 平方尺,
平方尺,![[公式]](https://www.zhihu.com/equation?tex=1%5Csim+2) 尺边长的正方形面积为
尺边长的正方形面积为![[公式]](https://www.zhihu.com/equation?tex=1%5Csim+4) 平方尺:
平方尺:
 同样,根据不充分理由原则,
同样,根据不充分理由原则,![[公式]](https://www.zhihu.com/equation?tex=1%5Csim+9) 平方尺之间的正方面面积是等可能的,那么正方形面积在
平方尺之间的正方面面积是等可能的,那么正方形面积在![[公式]](https://www.zhihu.com/equation?tex=1%5Csim+4) 平方尺之间的概率为
平方尺之间的概率为![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B3%7D%7B8%7D) :
:
 选择对“长度”还是对“面积”运用不充分理由原则,同一个问题会得到了不同的概率:
选择对“长度”还是对“面积”运用不充分理由原则,同一个问题会得到了不同的概率:
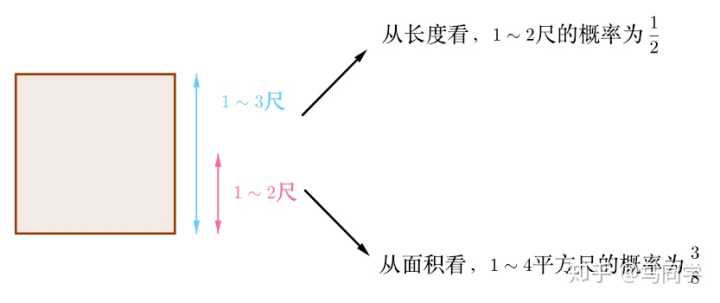 那么哪个是对的?
3 现代概率论
3.1 反思
19世纪不少人相信只要找到适当的等概率,就可以得到问题的唯一解。直到贝特朗悖论出现,人们才开始反思古典概率中的不合理之处:“等概率”的描述实在是太模糊了,存在歧义。
在后来数学家的不断努力中,概率论变得越来越严谨,大学中学习的公理化的现代概率论就是集大成者。
下面用现代的概率论重新来审视贝特朗悖论,你会发现其实根本没有矛盾之处。
3.2 重解贝特朗悖论
问:有一家锯木厂,它会把木头切成不同的木方,木方的截面都是正方形,边长会在
那么哪个是对的?
3 现代概率论
3.1 反思
19世纪不少人相信只要找到适当的等概率,就可以得到问题的唯一解。直到贝特朗悖论出现,人们才开始反思古典概率中的不合理之处:“等概率”的描述实在是太模糊了,存在歧义。
在后来数学家的不断努力中,概率论变得越来越严谨,大学中学习的公理化的现代概率论就是集大成者。
下面用现代的概率论重新来审视贝特朗悖论,你会发现其实根本没有矛盾之处。
3.2 重解贝特朗悖论
问:有一家锯木厂,它会把木头切成不同的木方,木方的截面都是正方形,边长会在![[公式]](https://www.zhihu.com/equation?tex=a%5Csim+b) 尺之间随机浮动:
尺之间随机浮动:
 也就是说木方的边长是一个随机变量
也就是说木方的边长是一个随机变量![[公式]](https://www.zhihu.com/equation?tex=X) ,符合均匀分布(均匀分布就是等概率的意思):
,符合均匀分布(均匀分布就是等概率的意思):
![[公式]](https://www.zhihu.com/equation?tex=X%5Csim+U%EF%BC%88a%2Cb%29%2C%5Cquad+%280+%3C+a+%3C+b%29%5C%5C) 那么:
那么:
![[公式]](https://www.zhihu.com/equation?tex=%5Cquad) (1)该锯木厂生产出来的正方形边长在
(1)该锯木厂生产出来的正方形边长在![[公式]](https://www.zhihu.com/equation?tex=c%5Csim+d) 尺之间的概率为多少(其中
尺之间的概率为多少(其中![[公式]](https://www.zhihu.com/equation?tex=a+%3C+c+%3C+d+%3C+b) )?
)?
![[公式]](https://www.zhihu.com/equation?tex=%5Cquad) (2)它的面积
(2)它的面积![[公式]](https://www.zhihu.com/equation?tex=Y%3DX%5E2) 又符合什么分布呢?
解:(1)记
又符合什么分布呢?
解:(1)记![[公式]](https://www.zhihu.com/equation?tex=X) 的累积分布函数为
的累积分布函数为![[公式]](https://www.zhihu.com/equation?tex=F_X%28x%29) ,其概率密度函数为
,其概率密度函数为![[公式]](https://www.zhihu.com/equation?tex=p_X%28x%29) ,因为
,因为![[公式]](https://www.zhihu.com/equation?tex=X%5Csim+U%EF%BC%88a%2Cb%29) ,所以:
,所以:
![[公式]](https://www.zhihu.com/equation?tex=+p_X%28x%29%3D+%5Cbegin%7Bcases%7D+++++%5Cfrac%7B1%7D%7Bb-a%7D%2C+%26a+%3C+x+%3C+b%5C%5C+++++0%2C+%26+%E5%85%B6%E5%AE%83+%5Cend%7Bcases%7D+%5C%5C) 那么要求的正方形边长在
那么要求的正方形边长在![[公式]](https://www.zhihu.com/equation?tex=c%5Csim+d) 尺之间的概率为:
尺之间的概率为:
![[公式]](https://www.zhihu.com/equation?tex=P%28c%5Cle+X%5Cle+d%29%3D%5Cint_c%5Ed+p_X%28x%29%5Cmathrm%7Bd%7Dx%3D%5Cfrac%7Bd-c%7D%7Bb-a%7D%5C%5C)
![[公式]](https://www.zhihu.com/equation?tex=%5Cquad) (2)假设
(2)假设![[公式]](https://www.zhihu.com/equation?tex=Y) 的累积分布函数为
的累积分布函数为![[公式]](https://www.zhihu.com/equation?tex=F_Y%28y%29) ,其概率密度函数为
,其概率密度函数为![[公式]](https://www.zhihu.com/equation?tex=p_Y%28y%29) 。先来求
。先来求![[公式]](https://www.zhihu.com/equation?tex=F_Y%28y%29) :
:
![[公式]](https://www.zhihu.com/equation?tex=%5Cbegin%7Baligned%7D+F_Y%28y%29+++++%26%3DP%28Y%5Cle+y%29%3DP%28X%5E2%5Cle+y%29+%5C%5C+++++%5C%5C+++++%26%3DP%28X%5Cle+%5Csqrt%7By%7D%29%3DF_X%28%5Csqrt%7By%7D%29+%5Cend%7Baligned%7D+%5C%5C) 将
将![[公式]](https://www.zhihu.com/equation?tex=F_Y%28y%29) 对
对![[公式]](https://www.zhihu.com/equation?tex=y) 求导就得到了概率密度函数,也就是得到了
求导就得到了概率密度函数,也就是得到了![[公式]](https://www.zhihu.com/equation?tex=Y) 的分布:
的分布:
![[公式]](https://www.zhihu.com/equation?tex=+%5Cbegin%7Baligned%7D+p_Y%28y%29+++++%26%3D%5Cfrac%7B%5Cmathrm%7Bd%7D%7D%7B%5Cmathrm%7Bd%7Dy%7DF_Y%28y%29%3D%5Cfrac%7B%5Cmathrm%7Bd%7D%7D%7B%5Cmathrm%7Bd%7Dy%7DF_X%28%5Csqrt%7By%7D%29%5C%5C+++++%5C%5C+++++%26%3D%5Cfrac%7B%5Cmathrm%7Bd%7D+F_X%28%5Csqrt%7By%7D%29%7D%7B%5Cmathrm%7Bd%7D%5Cleft%28%5Csqrt%7By%7D%5Cright%29%7D%5Cfrac%7B%5Cmathrm%7Bd%7D%5Csqrt%7By%7D%7D%7B%5Cmathrm%7Bd%7Dy%7D%26%26%E9%93%BE%E5%BC%8F%E6%B3%95%E5%88%99%5C%5C+++++%5C%5C+++++%26%3D%5Cfrac%7B1%7D%7B2%5Csqrt%7By%7D%7Dp_X%28%5Csqrt%7By%7D%29%5C%5C+++++%5C%5C+++++%26%3D+++++%5Cbegin%7Bcases%7D+++++++++%5Cfrac%7B1%7D%7B2%5Csqrt%7By%7D%7D%5Ccdot%5Cfrac%7B1%7D%7Bb-a%7D%2C+%26a+%3C+%5Csqrt%7By%7D+%3C+b%5C%5C+++++++++0%2C+%26+%E5%85%B6%E5%AE%83+++++%5Cend%7Bcases%7D%5C%5C+++++%5C%5C+++++%26%3D+++++%5Cbegin%7Bcases%7D+++++++++%5Cfrac%7B1%7D%7B2%5Csqrt%7By%7D%28b-a%29%7D%2C+%26a%5E2+%3C+y+%3C+b%5E2%5C%5C+++++++++0%2C+%26+%E5%85%B6%E5%AE%83+++++%5Cend%7Bcases%7D%5C%5C+%5Cend%7Baligned%7D+%5C%5C) (1)(2)两个问题回答下来,可见边长符合均匀分布时,面积并不符合均匀分布。
4 总结
贝特朗悖论产生的原因在于,古典概率中的“等概率”非常模糊:
(1)(2)两个问题回答下来,可见边长符合均匀分布时,面积并不符合均匀分布。
4 总结
贝特朗悖论产生的原因在于,古典概率中的“等概率”非常模糊:
- 边长的分布是未知的,所以是等概率的
- 面积的分布是未知的,所以是等概率的
进而导出了矛盾。现代概率论通过分布来描述边长的随机性后,这种模糊性消失了,贝特朗悖论中的矛盾也就不存在的。
同学们还可以试试假设面积符合均匀分布,试求一下边长符合什么分布。 本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。



















