排列组合中有很多恒等式,比如 ![[公式]](https://www.zhihu.com/equation?tex=C_%7Bn%7D%5E%7Bm%7D%2BC_%7Bn%7D%5E%7Bm-1%7D%3DC_%7Bn%2B1%7D%5E%7Bm%7D) 。刚接触时,我们往往把它们当作公式来记忆,利用
。刚接触时,我们往往把它们当作公式来记忆,利用 ![[公式]](https://www.zhihu.com/equation?tex=P_%7Bn%7D%5E%7Bm%7D%3D%5Cfrac%7Bn+%21%7D%7B%28n-m%29+%21%7D) 和
和 ![[公式]](https://www.zhihu.com/equation?tex=C_n%5Em%3D%5Cfrac%7Bn+%21%7D%7Bm+%21+%5Ccdot%28n-m%29+%21%7D) 来证明。但其实,它们都可以被赋予具体的场景(或问题),通过“算两次”的技巧来验证和理解,比如上述恒等式左右两边都是指从
来证明。但其实,它们都可以被赋予具体的场景(或问题),通过“算两次”的技巧来验证和理解,比如上述恒等式左右两边都是指从 ![[公式]](https://www.zhihu.com/equation?tex=n%2B1) 个人中选出
个人中选出 ![[公式]](https://www.zhihu.com/equation?tex=m) 个人的方法数。
本文从计数原理出发讲解排列与组合公式的由来,并在此基础上讲解如何通过具体的场景来理解各种不同的排列组合恒等式,比如
个人的方法数。
本文从计数原理出发讲解排列与组合公式的由来,并在此基础上讲解如何通过具体的场景来理解各种不同的排列组合恒等式,比如
![[公式]](https://www.zhihu.com/equation?tex=C_%7Bn%7D%5E%7B0%7D%2BC_%7Bn%7D%5E%7B1%7D%2B%5Ccdots%2BC_%7Bn%7D%5E%7Bn%7D%3D2%5E%7Bn%7D) ;
;
![[公式]](https://www.zhihu.com/equation?tex=C_%7Br%7D%5E%7Br%7D%2BC_%7Br%2B1%7D%5E%7Br%7D%2B%5Ccdots%2BC_%7Bn%7D%5E%7Br%7D%3DC_%7Bn%2B1%7D%5E%7Br%2B1%7D) ;
;
![[公式]](https://www.zhihu.com/equation?tex=C_%7Bm%7D%5E%7Br%7D+C_%7Bn%7D%5E%7B0%7D%2BC_%7Bm%7D%5E%7Br-1%7D+C_%7Bn%7D%5E%7B1%7D%2B%5Ccdots%2BC_%7Bm%7D%5E%7B0%7D+C_%7Bn%7D%5E%7Br%7D%3DC_%7Bn%2Bm%7D%5E%7Br%7D) ;
;
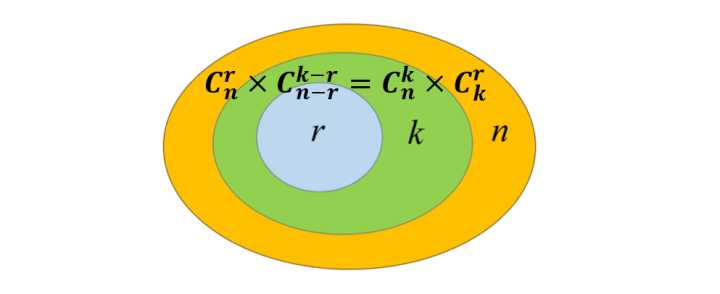
![[公式]](https://www.zhihu.com/equation?tex=C_%7Bn%7D%5E%7Br%7D+%5Ctimes+C_%7Bn-r%7D%5E%7Bk-r%7D%3DC_%7Bn%7D%5E%7Bk%7D+%5Ctimes+C_%7Bk%7D%5E%7Br%7D) ……
希望与大家探讨和加深对排列组合恒等式的理解。
主要内容:
……
希望与大家探讨和加深对排列组合恒等式的理解。
主要内容:
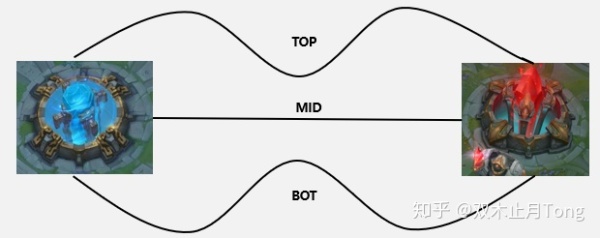
![[公式]](https://www.zhihu.com/equation?tex=1%2B1%2B1%3D3) 种。这就是加法原理。
但如果你从蓝色水晶出发先到河道,然后再从河道出发前往红色水晶那有多少种走法呢?
种。这就是加法原理。
但如果你从蓝色水晶出发先到河道,然后再从河道出发前往红色水晶那有多少种走法呢?
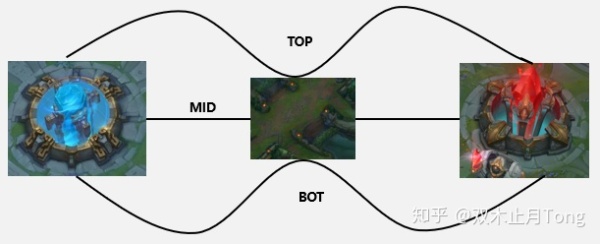
![[公式]](https://www.zhihu.com/equation?tex=3%5Ctimes3%3D9) 种走法。这就是乘法原理:如果做一件事情需要“分步进行”,那么总的方法数就等于把每一步骤的方法数乘在一起。
种走法。这就是乘法原理:如果做一件事情需要“分步进行”,那么总的方法数就等于把每一步骤的方法数乘在一起。

图:加法原理与乘法原理 
![[公式]](https://www.zhihu.com/equation?tex=n) 个人中挑选
个人中挑选 ![[公式]](https://www.zhihu.com/equation?tex=m) 个人排成一排,有多少种方法数呢?
个人排成一排,有多少种方法数呢?

![[公式]](https://www.zhihu.com/equation?tex=m) 个人,也就有
个人,也就有 ![[公式]](https://www.zhihu.com/equation?tex=m) 个位置,不妨一个一个位置来考虑:第一个位置有
个位置,不妨一个一个位置来考虑:第一个位置有 ![[公式]](https://www.zhihu.com/equation?tex=n) 种选择;第二个位置有
种选择;第二个位置有 ![[公式]](https://www.zhihu.com/equation?tex=%28n-1%29) 种选择;……第
种选择;……第 ![[公式]](https://www.zhihu.com/equation?tex=m) 个位置有
个位置有 ![[公式]](https://www.zhihu.com/equation?tex=%28n-m%2B1%29) 种选择。
所以一共有
种选择。
所以一共有 ![[公式]](https://www.zhihu.com/equation?tex=n%5Ccdot+%28n-1%29%5Ccdot%28n-2%29%5Ccdots%28n-m%2B1%29) 种方法数,记为
种方法数,记为 ![[公式]](https://www.zhihu.com/equation?tex=P_n%5Em) 。
。
![[公式]](https://www.zhihu.com/equation?tex=n) ,
,![[公式]](https://www.zhihu.com/equation?tex=n+%21%3Dn%28n-1%29%28n-2%29%28n-3%29+%5Cdots+%5Ctimes+3+%5Ctimes+2+%5Ctimes+1) ,
并且规定
,
并且规定 ![[公式]](https://www.zhihu.com/equation?tex=0%21%3D1) .
.
![[公式]](https://www.zhihu.com/equation?tex=P_%7Bn%7D%5E%7Bm%7D%3D%5Cfrac%7Bn+%21%7D%7B%28n-m%29+%21%7D) 。
特别的,当
。
特别的,当 ![[公式]](https://www.zhihu.com/equation?tex=m%3Dn) 时,也就是
时,也就是 ![[公式]](https://www.zhihu.com/equation?tex=n) 个人全部排队,也叫做全排列,
个人全部排队,也叫做全排列, ![[公式]](https://www.zhihu.com/equation?tex=P_n%5En%3Dn%21) 。
接着考虑组合(Combination)。
让我们再回到上面一个问题:请问从
。
接着考虑组合(Combination)。
让我们再回到上面一个问题:请问从 ![[公式]](https://www.zhihu.com/equation?tex=n) 个人中挑选
个人中挑选 ![[公式]](https://www.zhihu.com/equation?tex=m) 个人排成一排,有多少种方法数呢?
前面我们是通过从整体出发一个位置一个位置的考虑得到了排列数,接下去可以换一种思路:我们先从
个人排成一排,有多少种方法数呢?
前面我们是通过从整体出发一个位置一个位置的考虑得到了排列数,接下去可以换一种思路:我们先从 ![[公式]](https://www.zhihu.com/equation?tex=n) 个人中选出
个人中选出 ![[公式]](https://www.zhihu.com/equation?tex=m) 个人,然后再对这
个人,然后再对这 ![[公式]](https://www.zhihu.com/equation?tex=m) 个人进行排列。因为完成的是同一件事情所以方法数肯定是相等的,且我们把从
个人进行排列。因为完成的是同一件事情所以方法数肯定是相等的,且我们把从![[公式]](https://www.zhihu.com/equation?tex=n) 个人中选出
个人中选出 ![[公式]](https://www.zhihu.com/equation?tex=m) 个人记为
个人记为 ![[公式]](https://www.zhihu.com/equation?tex=C_n%5Em) ,那么根据分步原理可知:
,那么根据分步原理可知:
![[公式]](https://www.zhihu.com/equation?tex=C_n%5Em%5Ccdot+P_m%5Em%3DP_n%5Em) 于是,
于是,
![[公式]](https://www.zhihu.com/equation?tex=C_%7Bn%7D%5E%7Bm%7D%3D%5Cfrac%7Bn+%21%7D%7B%28n-m%29+%21+m+%21%7D) 。
。
![[公式]](https://www.zhihu.com/equation?tex=C_n%5Em%3DC_n%5E%7Bn-m%7D)
![[公式]](https://www.zhihu.com/equation?tex=P_%7Bn%7D%5E%7Bm%7D%2Bm+P_%7Bn%7D%5E%7Bm-1%7D%3DP_%7Bn%2B1%7D%5E%7Bm%7D)
![[公式]](https://www.zhihu.com/equation?tex=C_%7Bn%7D%5E%7Bm%7D%2BC_%7Bn%7D%5E%7Bm-1%7D%3DC_%7Bn%2B1%7D%5E%7Bm%7D)
![[公式]](https://www.zhihu.com/equation?tex=C_%7Br%7D%5E%7Br%7D%2BC_%7Br%2B1%7D%5E%7Br%7D%2B%5Ccdots%2BC_%7Bn%7D%5E%7Br%7D%3DC_%7Bn%2B1%7D%5E%7Br%2B1%7D)
![[公式]](https://www.zhihu.com/equation?tex=C_%7Bn%7D%5E%7Bm%2B1%7D%2BC_%7Bn%7D%5E%7Bm-1%7D%2B2+C_%7Bn%7D%5E%7Bm%7D%3DC_%7Bn%2B2%7D%5E%7Bm%2B1%7D)
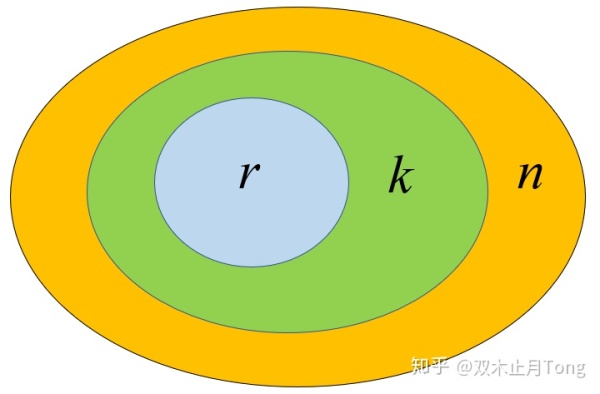
![[公式]](https://www.zhihu.com/equation?tex=C_%7Bn%7D%5E%7Br%7D+%5Ctimes+C_%7Bn-r%7D%5E%7Bk-r%7D%3DC_%7Bn%7D%5E%7Bk%7D+%5Ctimes+C_%7Bk%7D%5E%7Br%7D)
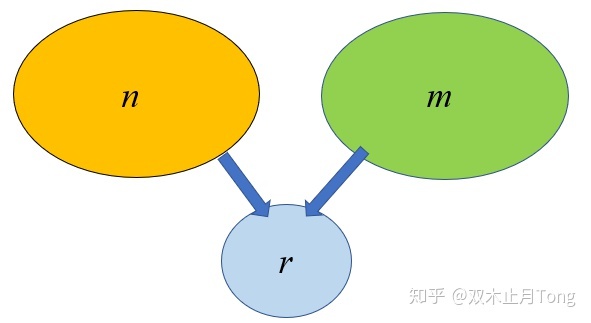
![[公式]](https://www.zhihu.com/equation?tex=C_%7Bm%7D%5E%7Br%7D+C_%7Bn%7D%5E%7B0%7D%2BC_%7Bm%7D%5E%7Br-1%7D+C_%7Bn%7D%5E%7B1%7D%2B%5Ccdots%2BC_%7Bm%7D%5E%7B0%7D+C_%7Bn%7D%5E%7Br%7D%3DC_%7Bn%2Bm%7D%5E%7Br%7D)
![[公式]](https://www.zhihu.com/equation?tex=m%3Dn) 时有
时有
![[公式]](https://www.zhihu.com/equation?tex=C_%7Bn%7D%5E%7Br%7D+C_%7Bn%7D%5E%7B0%7D%2BC_%7Bn%7D%5E%7Br-1%7D+C_%7Bn%7D%5E%7B1%7D%2B%5Ccdots%2BC_%7Bn%7D%5E%7B0%7D+C_%7Bn%7D%5E%7Br%7D%3DC_%7Bn%2Bn%7D%5E%7Br%7D%3DC_%7B2n%7D%5Er) 又根据恒等式(1)
又根据恒等式(1) ![[公式]](https://www.zhihu.com/equation?tex=C_n%5Ei%3DC_n%5E%7Bn-i%7D) ,所以下式成立:
(6*)
,所以下式成立:
(6*) ![[公式]](https://www.zhihu.com/equation?tex=%5Cleft%28C_%7Bn%7D%5E%7B0%7D%5Cright%29%5E%7B2%7D%2B%5Cleft%28C_%7Bn%7D%5E%7B1%7D%5Cright%29%5E%7B2%7D%2B%5Ccdots%2B%5Cleft%28C_%7Bn%7D%5E%7Br%7D%5Cright%29%5E%7B2%7D%3DC_%7B2+n%7D%5E%7Br%7D) (7)
(7) ![[公式]](https://www.zhihu.com/equation?tex=C_%7Bn%7D%5E%7B0%7D%2BC_%7Bn%7D%5E%7B1%7D%2B%5Ccdots%2BC_%7Bn%7D%5E%7Bn%7D%3D2%5E%7Bn%7D)
![[公式]](https://www.zhihu.com/equation?tex=C_%7Bn%7D%5E%7B1%7D%2B2+C_%7Bn%7D%5E%7B2%7D%2B%5Ccdots%2Bn+C_%7Bn%7D%5E%7Bn%7D%3Dn+2%5E%7Bn-1%7D) ,但是这个暂时还没有想到如何用一个具体问题来理解它。
,但是这个暂时还没有想到如何用一个具体问题来理解它。

![[公式]](https://www.zhihu.com/equation?tex=C_%7Bn%7D%5E%7B1%7D%2B2+C_%7Bn%7D%5E%7B2%7D%2B%5Ccdots%2Bn+C_%7Bn%7D%5E%7Bn%7D%3Dn+2%5E%7Bn-1%7D) 感谢
的评论:
感谢
的评论:
(1)计数原理 (2)排列组合 (3)恒等式
一、计数原理
计数原理就是计数的方法,一共有两种原理:加法原理与乘法原理 接下里我们借助召唤师峡谷或者王者峡谷进行说明: 如果做一件事情是“一步到位”,那么我们就用加法原理。 从蓝色水晶沿着“上中下”三条路到红色水晶有多少种走法呢?



注:两种思想在数学中都很常见,之前有一篇《分类讨论》就详细讲解了运用分类讨论解题。
二、排列组合
介绍完计数原理那么我们就可以来讲讲排列组合了。首先是排列(Permutation)。 请问从
注:排列数有不同的表示方法,如上面写的太复杂了,所以我们引入了阶乘(Factorial):对于任一自然数等,不过表达的含义是一样的。
注:这下4个0也可以算24点了,所以计算式就可以简写为:
注: (1)组合数也有很多中表示方法,比如,但是含义是相同的; (2)排列是有顺序的,组合是没有顺序的,所以看问题时一定要考虑清楚。
三、恒等式
至此,我们已经把排列数与组合数计算公式都讲清楚了,接下去就是要讲排列组合中各种恒等式了。 在前言中我们也讲了,本文主要是通过赋予恒等式具体含义来深入理解其成立原因,而不是通过带入排列数或组合数计算公式进行证明。所以关键的点不在于代数计算而是理解含义。 (1)左边表达的是从这就是“算两次”的技巧,从不同角度去思考问题,因为是同一件事情所以得到的式子都是相等的。 (2)个人中选择
个人参加活动;右边表示的是从
个人中选择
个人不参加活动。左右两式表示的都是同一件事情的方法数,所以相等。
右边表示的是从这里我们通过对特定的人“小黑”进行分类讨论得到了同一件事情的总方法数的不同表达式,而接下去讲的恒等式都是用这种方法说明的。这有助于我们深入理解这些恒等式。 (3)个人中选择
个人进行排队; 针对上述这件事,我们考虑
中特定的一个人“小黑”的情况: 1)如果小黑不在这
个人的队列中,那么有
种方法; 2)如果小黑在这
个人的队列中。那么先把小黑安置好,可以从
个位置中任意选一个位置,然后再从剩下的
个人中选择
个人排到队伍中。因此总的方法数为
。 根据加法原理,所以这件事总的方法数为
,得证。
右式表示的是从特别的,可以用恒等式(3)来证明: (3*)个人中选出
个人; 左式我们可以按照恒等式(2)进行类似的分类讨论,指定一个人“小黑”: 1)如果小黑在这
个人中,那么再从
个人中选
个人; 2)如果小黑不在这
个人中,那么就是从
个人中选
个人;根据加法原理,这件事总的方法数为:
,得证。
因为(4), 所以
(利用恒等式(3))。 接着
…… 依次下去,最后可得
,得证。
右式表示的是从下面再来看一些稍微复杂的。 (5)个人中选出
个人; 与上面讨论类似,左边需要根据“小黑”、“小白”两个人的情况进行分类讨论: 1)小黑、小白都没有被挑选出来,
; 2)小黑、小白都被挑选出来了,
; 3)小黑、小白其中有一人被挑选出来了,
。 所以,根据加法原理
,得证。 注:这里麻烦了一点,需要讨论两个人的情况,不过思想还是和前面一样的。按照这种想法我们能够造出很多很多的组合恒等式。

下面考虑这样一件事的方案数: 在(6)个人中有
个人中奖,并且中奖的
个人中有
个人为特等奖; 右式是这样考虑的:先从
个人中选择
个人中奖,然后再从
个人中选择
个人为特等奖,根据乘法原理
; 左式是这样考虑的:从
个人先把特等奖的
个人选出来,然后再选
个中奖者,根据乘法原理
。 因此左式等于右式。

下面考虑这样一件事的方案数: 有黄、绿两支队伍,分别有特别的,当个人,现在选拔
个人组成新的一支蓝队。 右式是这样考虑的,先把两支队伍合在一起,一共
个人,然后从中选出
个人,所以方案数为
; 左式,既然有两支队伍,那么就根据两支队伍入选的人数进行分类讨论: 1)黄队入选
个,绿队入选
个,
; 2)黄队入选
个,绿队入选
个,
; …… 根据加法原理,一共有
种方案数。 因此左式等于右式。
下面考虑这样一个问题: 请问含个元素的集合
的子集有多少个? 左边:我们可以按照子集中元素的个数进行分类讨论, 1)有0个元素的子集有
个; 2)有1个元素的子集有
个; …… 根据加法原理,子集一共有
个。 右边:我们也可以按照每个元素进行讨论,对于每一个元素而言它都有两种选择:属于这个子集与不属于这个子集,所以根据乘法原理,
。 因此,左式等于右式。
总结
组合恒等式还有很多,比如注:上述恒等式的代数证明会用到:如果我们拿到恒等式后能够想想它的“含义”还挺有趣的,就像在第三部分给出的那样,不仅能够加深我们对排列组合的理解还能够锻炼思维、拓展思路。 比较直接的影响就是:做题的时候如果认识这个恒等式,那会方便不少。比如:。于是,
(根据恒等式(7))

根据有兴趣的可以思考下面这个恒等式,怎么样给它一个合理的解释呢?, 所以
。 那么问题就变成问
的最后两位是多少,就是一个很纯粹的数论取余的问题了:
因为
所以,
注:数论的内容我们之后再分享。
小罗非鱼
可以把上面式子两边都除以感觉挺有道理的,不知道大家觉得如何?![[公式]](https://www.zhihu.com/equation?tex=2%5En)
那么左式为
元集合子集元素个数的平均数;而右边对于单个元素而言“在子集中”与“不在子集中”的概率都为
,所以子集中元素个数平均数为
.
本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。