作者:Bazinga
可以相交. 这里举一个水平渐近线(horizontal asymptote)的例子. 水平渐近线的定义如下:
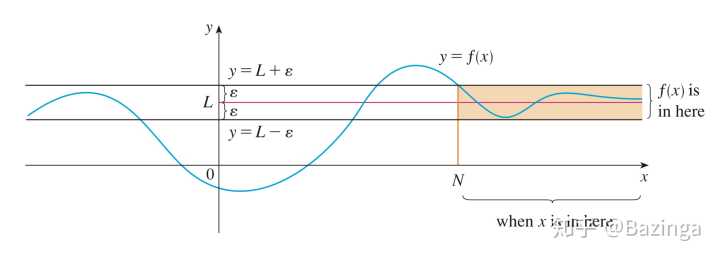
图示(来自Calculus Early Transcendentals ed8, Jame Stewart ) ![[公式]](https://www.zhihu.com/equation?tex=f) 在无穷远时的行为,在任何有限的区间内函数
在无穷远时的行为,在任何有限的区间内函数 ![[公式]](https://www.zhihu.com/equation?tex=f) 的行为都无足轻重. 在图示中,函数
的行为都无足轻重. 在图示中,函数 ![[公式]](https://www.zhihu.com/equation?tex=f) 和
和 ![[公式]](https://www.zhihu.com/equation?tex=L) 相交了不止一次,然而这仍然不会改变
相交了不止一次,然而这仍然不会改变 ![[公式]](https://www.zhihu.com/equation?tex=L) 是
是 ![[公式]](https://www.zhihu.com/equation?tex=f) 的渐近线这一事实. 只要函数满足
的渐近线这一事实. 只要函数满足 ![[公式]](https://www.zhihu.com/equation?tex=%5Clim_%7Bx+%5Crightarrow+%5Cinfty%7D%7Bf%28x%29%7D%3DL) , 那么
, 那么 ![[公式]](https://www.zhihu.com/equation?tex=L) 就是函数
就是函数 ![[公式]](https://www.zhihu.com/equation?tex=f) 的渐近线.
当然图中的函数可能是随便画的,下面举一个例子.
考虑函数
的渐近线.
当然图中的函数可能是随便画的,下面举一个例子.
考虑函数 ![[公式]](https://www.zhihu.com/equation?tex=f%28x%29%3De%5E%7B-x%7D%5Cmathbb%7Bsin%7D%28nx%29) , 其中
, 其中 ![[公式]](https://www.zhihu.com/equation?tex=n%5Cin+%5Cmathbb%7BZ%7D) . 下面证明该函数的渐近线
. 下面证明该函数的渐近线 ![[公式]](https://www.zhihu.com/equation?tex=L%3D0) .
证明: 由于
.
证明: 由于 ![[公式]](https://www.zhihu.com/equation?tex=-e%5E%7B-x%7D%3Ce%5E%7B-x%7D+%5Csin+%28n+x%29%3Ce%5E%7B-x%7D) ,
, ![[公式]](https://www.zhihu.com/equation?tex=%5Clim+_%7Bx+%5Crightarrow+%5Cinfty%7D+e%5E%7B-x%7D%3D%5Clim+_%7Bx+%5Crightarrow+%5Cinfty%7D%5Cleft%28-e%5E%7B-x%7D%5Cright%29%3D0) , 根据夹逼定理,
, 根据夹逼定理, ![[公式]](https://www.zhihu.com/equation?tex=%5Clim+_%7Bx+%5Crightarrow+%5Cinfty%7D+e%5E%7B-x%7D+%5Csin+%28n+x%29%3D0) .
. ![[公式]](https://www.zhihu.com/equation?tex=%5Csquare) 然而在Mathematica上画个图:
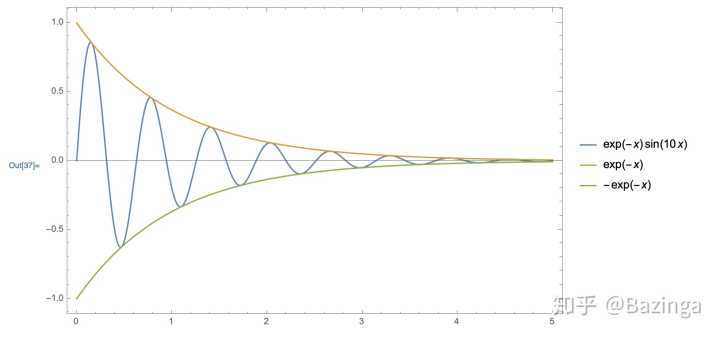
然而在Mathematica上画个图:
假设是一个在区间
的函数. 若对于所有的
都存在一个对应的
,使得如果
,则有
,则
称为函数
的水平渐近线.

Plot[{Exp[-x]*Sin[10 x], Exp[-x], -Exp[-x]}, {x, 0, 5},
PlotRange -> Full, PlotTheme -> "Detailed", GridLines -> None,
Axes -> True]
本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。