1 洛必达法则
![[公式]](https://www.zhihu.com/equation?tex=0%2F0) 型和
型和 ![[公式]](https://www.zhihu.com/equation?tex=%5Cinfty+%2F%5Cinfty+) 型时,有
型时,有 ![[公式]](https://www.zhihu.com/equation?tex=%7B%5Cdisplaystyle+%5Clim+_%7Bx%5Cto+a%7D%7B%5Cfrac%7Bf%28x%29%7D%7Bg%28x%29%7D%7D%3D%5Clim+_%7Bx%5Cto+a%7D%7B%5Cfrac%7Bf%27%28x%29%7D%7Bg%27%28x%29%7D%7D%7D) 。
可见,洛必达法则最犀利的是大大简化了极限运算。这种化繁为简的技术手段从来都是深受喜爱的。
这篇文章我们主要回答一下两个问题:
。
可见,洛必达法则最犀利的是大大简化了极限运算。这种化繁为简的技术手段从来都是深受喜爱的。
这篇文章我们主要回答一下两个问题:
![[公式]](https://www.zhihu.com/equation?tex=u%28x%29%3D%28g%28x%29%2Cf%28x%29%29) ,为了阅读顺畅,这个函数我要多解释下。
对于一般我们接触的函数,比如
,为了阅读顺畅,这个函数我要多解释下。
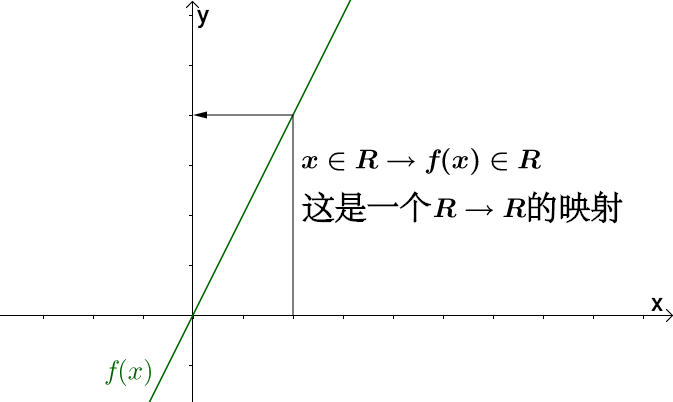
对于一般我们接触的函数,比如 ![[公式]](https://www.zhihu.com/equation?tex=f%28x%29%3D2x%2C+x%5Cin+R) ,根据函数定义,这是一个
,根据函数定义,这是一个 ![[公式]](https://www.zhihu.com/equation?tex=R%5Cto+R) 的映射:
的映射:
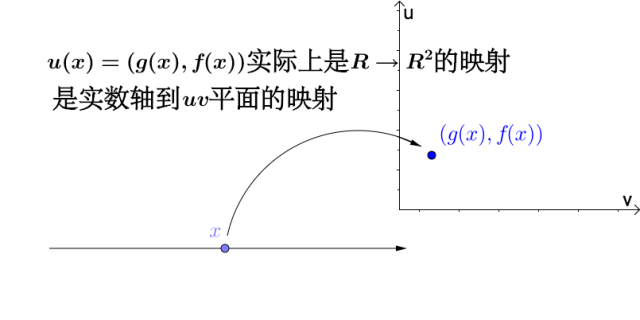
![[公式]](https://www.zhihu.com/equation?tex=u%28x%29%3D%28g%28x%29%2Cf%28x%29%29) 是一个
是一个 ![[公式]](https://www.zhihu.com/equation?tex=R%5Cto+R%5E2) 的映射:
的映射:
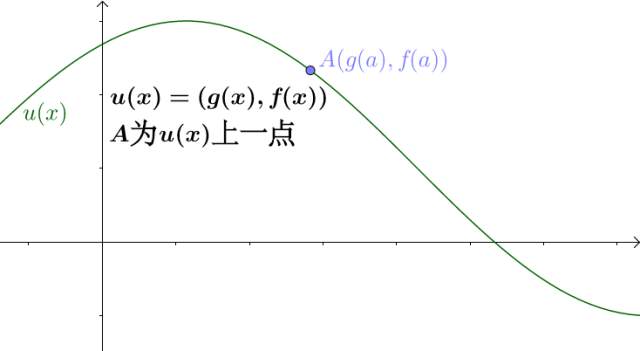
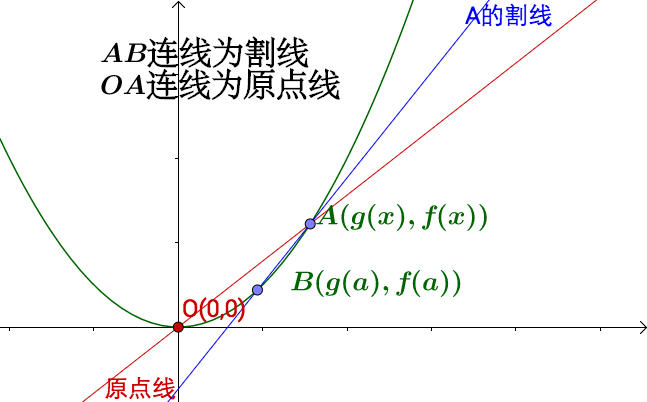
![[公式]](https://www.zhihu.com/equation?tex=u%28x%29%3D%28g%28x%29%2Cf%28x%29%29) 可以如下表示:
可以如下表示:
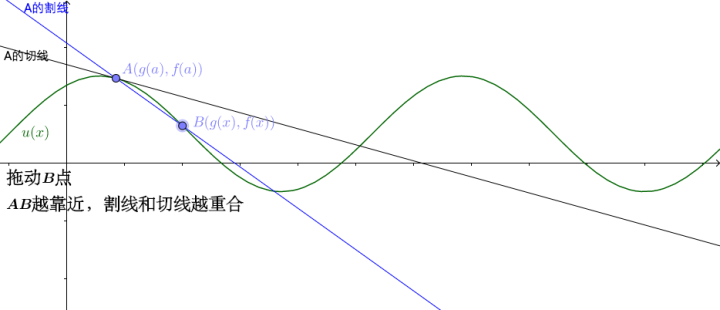
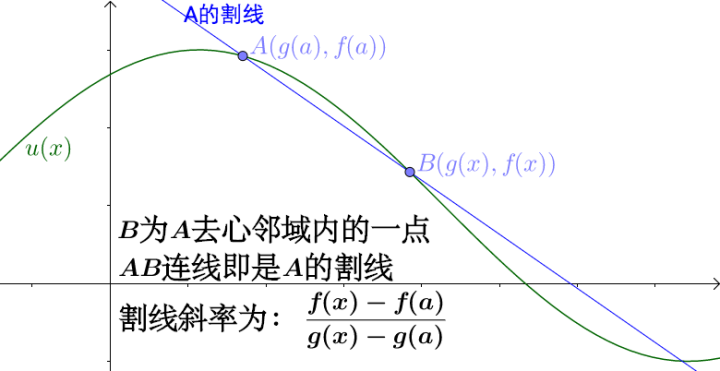
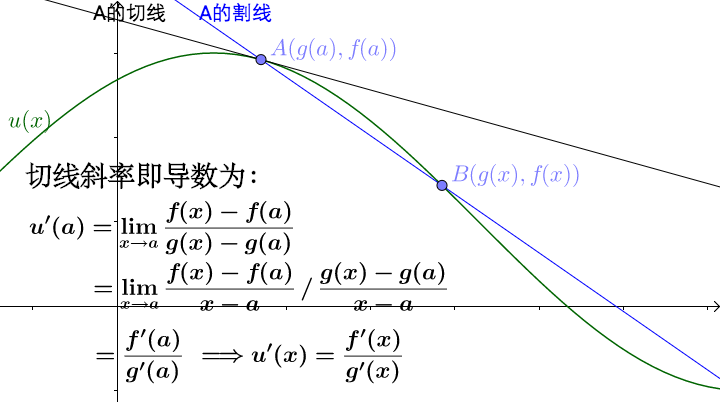
![[公式]](https://www.zhihu.com/equation?tex=A) 点的割线:
点的割线:
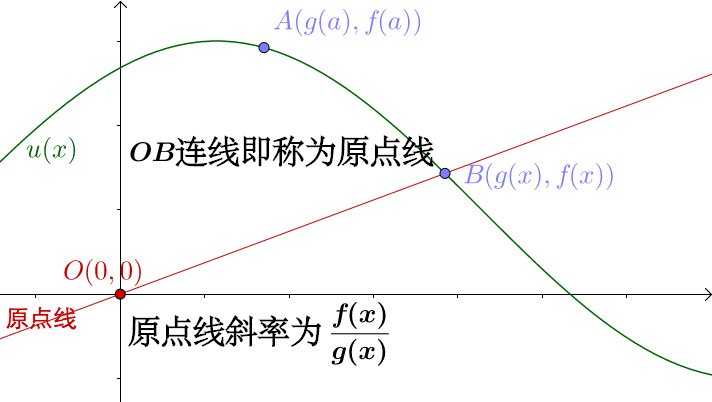
![[公式]](https://www.zhihu.com/equation?tex=O%280%2C0%29) 连接
连接 ![[公式]](https://www.zhihu.com/equation?tex=B) 点,马同学把这个连线称为原点线:
点,马同学把这个连线称为原点线:
![[公式]](https://www.zhihu.com/equation?tex=u%28x%29) 我们得到两个的结论:
我们得到两个的结论:
![[公式]](https://www.zhihu.com/equation?tex=u%27%28x%29%3D%5Cfrac%7Bf%27%28x%29%7D%7Bg%27%28x%29%7D)
![[公式]](https://www.zhihu.com/equation?tex=%7B%5Cdisplaystyle+%5Clim+_%7Bx%5Cto+a%7D%7B%5Cfrac%7Bf%28x%29%7D%7Bg%28x%29%7D%7D%3D%5Clim+_%7Bx%5Cto+a%7D%7B%5Cfrac%7Bf%27%28x%29%7D%7Bg%27%28x%29%7D%7D%7D) 。可见,构造关键函数之后,我们已经有了
。可见,构造关键函数之后,我们已经有了![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf%27%28x%29%7D%7Bg%27%28x%29%7D) 和
和 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf%28x%29%7D%7Bg%28x%29%7D) ,剩下的就是看这两者什么时候极限相等了?
1.2
,剩下的就是看这两者什么时候极限相等了?
1.2 ![[公式]](https://www.zhihu.com/equation?tex=0%2F0) 型
我们让
型
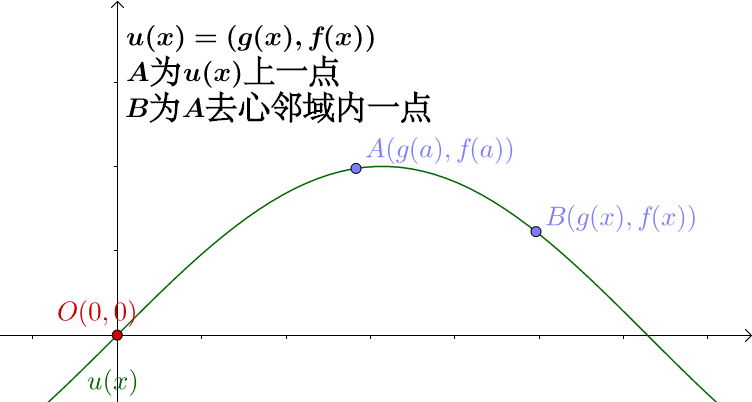
我们让 ![[公式]](https://www.zhihu.com/equation?tex=u%28x%29) 曲线可以经过
曲线可以经过 ![[公式]](https://www.zhihu.com/equation?tex=O%280%2C0%29) 点:
点:
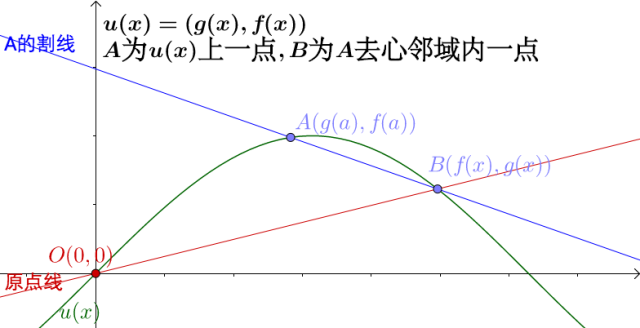
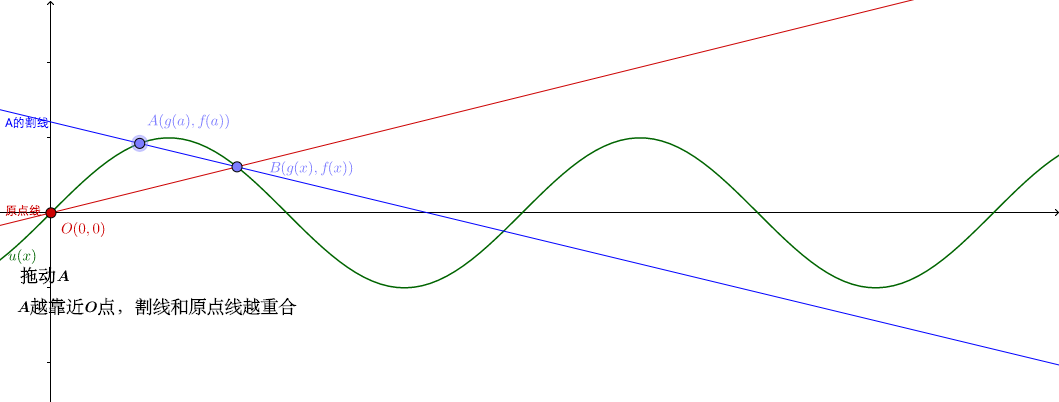
![[公式]](https://www.zhihu.com/equation?tex=A) 点越靠近原点,割线和原点线越接近:
点越靠近原点,割线和原点线越接近:
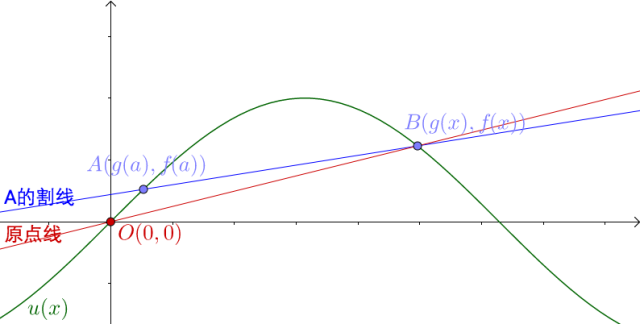
![[公式]](https://www.zhihu.com/equation?tex=A) 点和
点和 ![[公式]](https://www.zhihu.com/equation?tex=O) 点重合时,割线就是原点线:
点重合时,割线就是原点线:
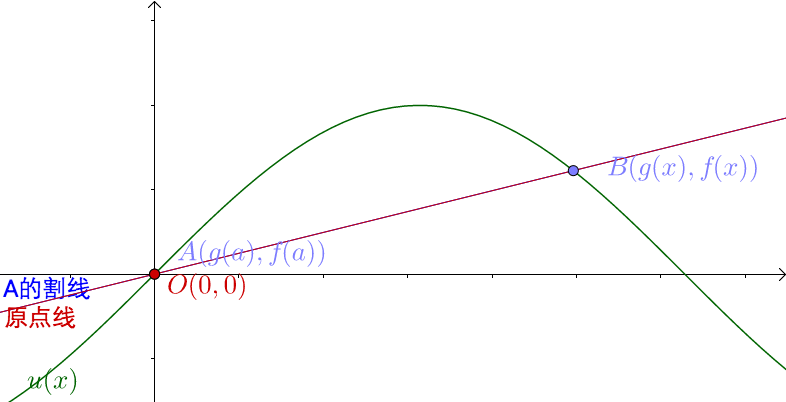
![[公式]](https://www.zhihu.com/equation?tex=A) 点和
点和 ![[公式]](https://www.zhihu.com/equation?tex=O) 点重合时,割线斜率就是原点线斜率,即
点重合时,割线斜率就是原点线斜率,即 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7Bf%28x%29%7D%7Bg%28x%29%7D) 。 根据割线的极限即切线,有
。 根据割线的极限即切线,有![[公式]](https://www.zhihu.com/equation?tex=%5Cdisplaystyle+%5Clim+_%7Bx%5Cto+a%7D%7B%5Cfrac%7Bf%28x%29%7D%7Bg%28x%29%7D%7D%3Du%27%28a%29) ,根据之前的结论有
,根据之前的结论有 ![[公式]](https://www.zhihu.com/equation?tex=u%27%28x%29%3D%5Cfrac%7Bf%27%28x%29%7D%7Bg%27%28x%29%7D) ,所以
,所以 ![[公式]](https://www.zhihu.com/equation?tex=%5Cdisplaystyle+u%27%28a%29%3D%5Clim+_%7Bx%5Cto+a%7D%7B%5Cfrac%7Bf%27%28x%29%7D%7Bg%27%28x%29%7D%7D) ,所以有
,所以有![[公式]](https://www.zhihu.com/equation?tex=%7B%5Cdisplaystyle+%5Clim+_%7Bx%5Cto+a%7D%7B%5Cfrac%7Bf%28x%29%7D%7Bg%28x%29%7D%7D%3D%5Clim+_%7Bx%5Cto+a%7D%7B%5Cfrac%7Bf%27%28x%29%7D%7Bg%27%28x%29%7D%7D%7D) ,即洛必达法则。
需要说明一点:
,即洛必达法则。
需要说明一点:
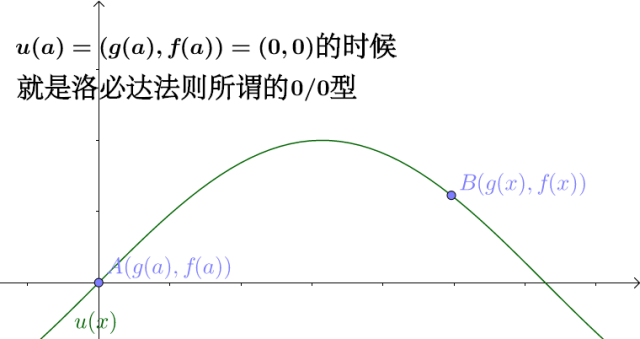
![[公式]](https://www.zhihu.com/equation?tex=0%2F0) 型可以生效。
1.3
型可以生效。
1.3 ![[公式]](https://www.zhihu.com/equation?tex=%5Cinfty+%2F%5Cinfty+) 型
在欧式几何中,两条线的斜率要相等,只有两种情况,重合或者平行。
这就是
型
在欧式几何中,两条线的斜率要相等,只有两种情况,重合或者平行。
这就是 ![[公式]](https://www.zhihu.com/equation?tex=%5Cinfty+%2F%5Cinfty+) 型为什么适用于洛必达法则的原因,我们来一起推导一下。
首先
型为什么适用于洛必达法则的原因,我们来一起推导一下。
首先 ![[公式]](https://www.zhihu.com/equation?tex=u%28x%29) 要换一下,必须得有
要换一下,必须得有 ![[公式]](https://www.zhihu.com/equation?tex=%28%5Cinfty+%2C%5Cinfty+%29) 点:
点:
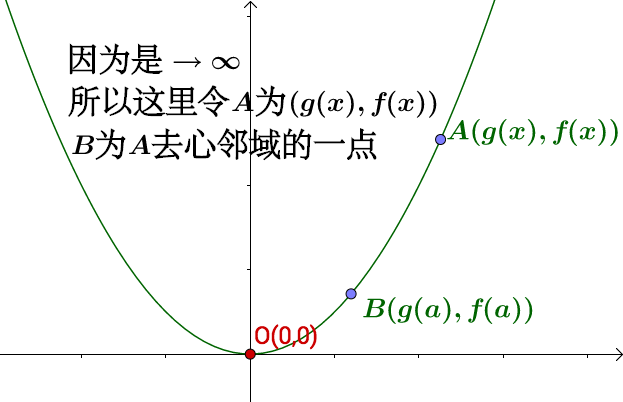
![[公式]](https://www.zhihu.com/equation?tex=A+%5Cto+%5Cinfty+) 时,割线和原点线趋向于平行:
时,割线和原点线趋向于平行:
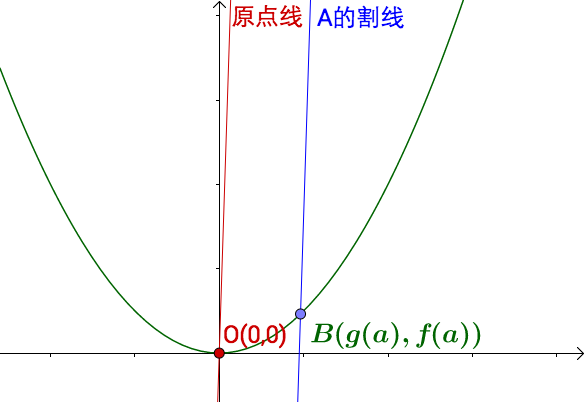
![[公式]](https://www.zhihu.com/equation?tex=A) 点,但是当
点,但是当 ![[公式]](https://www.zhihu.com/equation?tex=A+%5Cto+%5Cinfty+) 时居然两者可以平行。其实我们可以说两条平行线交于无穷远点,至于无穷远点能否到达又是另外的问题了。
你也可以动手试试
时居然两者可以平行。其实我们可以说两条平行线交于无穷远点,至于无穷远点能否到达又是另外的问题了。
你也可以动手试试
![[公式]](https://www.zhihu.com/equation?tex=A+%5Cto+%5Cinfty+) 意味着是
意味着是 ![[公式]](https://www.zhihu.com/equation?tex=%5Cinfty+%2F%5Cinfty+) 型。
根据
型。
根据 ![[公式]](https://www.zhihu.com/equation?tex=0%2F0) 型的推论的思路,洛必达法则对于
型的推论的思路,洛必达法则对于 ![[公式]](https://www.zhihu.com/equation?tex=%5Cinfty+%2F%5Cinfty+) 型也生效。
1.4 结论
所以洛必达法则生效的原因是:
型也生效。
1.4 结论
所以洛必达法则生效的原因是:
![[公式]](https://www.zhihu.com/equation?tex=g%28x%29%3D2x) ,
, ![[公式]](https://www.zhihu.com/equation?tex=f%28x%29%3D4x) ,可以用两种办法求极限:
,可以用两种办法求极限:
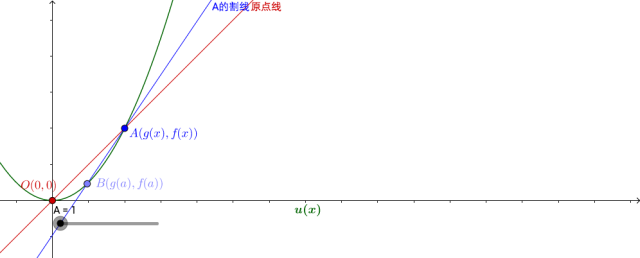
![[公式]](https://www.zhihu.com/equation?tex=u%28x%29%3D%28g%28x%29%2Cf%28x%29%29%3D%282x%2C4x%29) ,画出图像:
,画出图像:

![[公式]](https://www.zhihu.com/equation?tex=0%2F0) 型和
型和 ![[公式]](https://www.zhihu.com/equation?tex=%5Cinfty+%2F%5Cinfty+) 型最实用,但是好歹让马同学发明了一个马同学法则,希望可以像洛必达法则一样名垂千古。
作者:马同学
来源:知乎
型最实用,但是好歹让马同学发明了一个马同学法则,希望可以像洛必达法则一样名垂千古。
作者:马同学
来源:知乎
洛必达法则(l'Hôpital's rule)是利用导数来计算具有不定型的极限的方法。这法则是由瑞士数学家约翰·伯努利(Johann Bernoulli)所发现的,因此也被叫作伯努利法则(Bernoulli's rule)。维基百科不严格的说,洛必达法则就是在
- 为什么洛必达法则对于
型和
型生效?
- 洛必达法则对于别的类型是否生效?




所以可以得出切线的斜率即导数为:此处有互动内容,需要流量较大,最好有wifi处打开,土豪请随意。 点击此处前往操作。


- 原点线斜率为



此处有互动内容,需要流量较大,最好有wifi处打开,土豪请随意。 点击此处前往操作。





同样说明一下,此处有互动内容,需要流量较大,最好有wifi处打开,土豪请随意。 点击此处前往操作。
型:割线和原点线重合
型:割线和原点线平行
- 约分:
- 洛必达法则:

本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。