我是中科院物理所研究员叶方富,今天我给大家讲热力学第二定律。
在之前的热学课里,杨义峰老师已经给大家介绍了温度和热这两个非常重要的概念以及热力学第一定律。我们从中知道了,热的本质是什么。但是整个热力学框架里,还缺非常重要的一块,也就是热力学过程的一个方向性问题。热力学第二定律,正是这么一个描述方向性的规律。
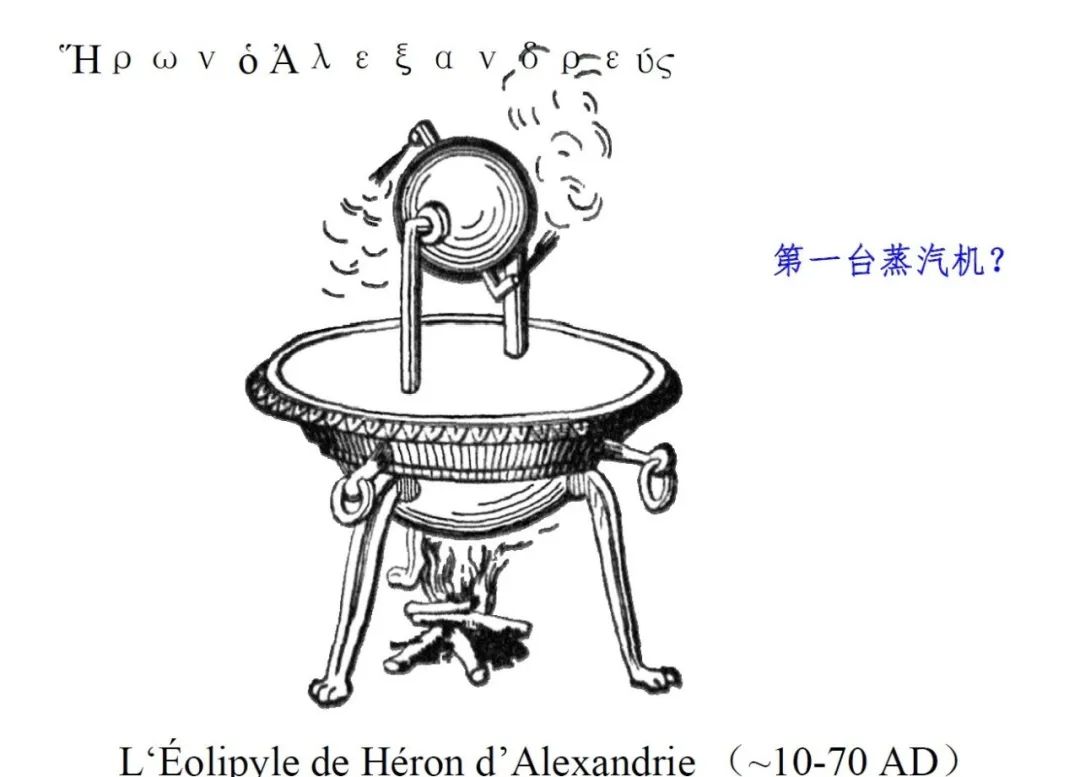
在正式介绍热力学第二定律的表述前,我们先看一下相关的背景。我们知道从18世纪60年代到19世纪中期,第一次工业革命轰轰烈烈地开展中。它开创了一个以机器来替代手工劳动的时代,是我们整个人类史发展的一次大飞跃。工业革命是以蒸汽机的广泛使用为标志的。这里我给大家看一下,这是一个蒸汽机模型,里面水烧开后,会产生蒸汽,然后蒸汽就会推动上面的轮子转动。当然这个模型是非常粗糙的。
在18、19世纪工业革命时候,得到广泛应用的是瓦特发明的蒸汽机。这个是瓦特当时制作的一个蒸汽机的模型。在蒸汽机得到广泛应用之后,当时大家会有一个非常重要的问题——怎么提高蒸汽机的效率。因为我们知道,当时在欧洲各个国家,工业上有各种各样的竞争,所以谁能开发出具有最高效率的蒸汽机,在整个竞争中,就会有非常大的优势。
这个问题当时是在一个纯粹的工业背景上提出来的。给出这个问题的解答的是卡诺。在前面杨老师的课上也给大家介绍过,卡诺是一个天才型的科学家,但是非常可惜的是,他很年轻的时候就去世了。他提出,我们现在叫卡诺热机,把整个蒸汽机工作的过程分解成四个过程:有两个等温过程、两个绝热过程。热机有两个热源,一个是高温热源,一个低温热源。
热机在高温热源的时候,它的第一个过程,就是从高温热源吸热,然后蒸汽保持等温膨胀的过程。它这里的压强跟整个体积是遵从等温膨胀的关系。在等温过程结束之后,然后紧接着热机离开了热源,它经历的是绝热膨胀过程,所以这时候它的压强跟它的体积遵循的是绝热膨胀的关系。在膨胀结束后,然后活塞又往里压气体,所以这时候它就会放热。在低温热源,先是一个等温放热的过程,最后是一个绝热压缩的过程。这四个过程组成了一个循环,我们叫做卡诺循环。
卡诺当时提出来,如果这四个过程都是可逆的话,这么一个抽象出来的蒸汽机,我们叫卡诺热机,它的效率是最高的 ,而且效率跟蒸汽机里面用的工作介质是没有关系的。它的整个效率,只和高温热源、低温热源的温度有关。但是就像我们刚才说的,很遗憾的是,卡诺他很年轻就去世了。那时候整个热力学第一定律,还没有得到很好的发展,当时认为热本身,是一种类似物质一样的存在,它本身是守恒的。
后来我们知道,焦耳等人发现热实际上不能按照热质说来解释,它实际上是一种能量的概念。热实际上是微观体系里的构成物质的分子的动能,包括势能的总和的体现。后来另外一个伟大的科学家克劳修斯也看到了卡诺相关的论述,他结合了后来发展出来的热力学第一定律,回头重新看卡诺定理的时候,发现要卡诺定理成立,这时候需要新补充一个定律,这就是现在被我们称为热力学第二定律的一个表述——热量从低温物体向高温物体传递而不引起其他任何影响是不可能的。
从表面上看这个结论感觉是一个比较显而易见的事情——热量只能从高温往低温传,就像水,只能从高处往低处流。这是我们对周围的现象的非常好的认识,但是你要把它表述准确到位,形成一种科学的表述,这里面很多东西还是很关键的。热力学第二定律不仅仅说热从低温到高温的物体的传递,很重要的一部分,大家看后面有一个界定,要不引起其它任何影响,一定要包括这一部分。
现在看我们身边的例子,热从低温到高温转移的例子是存在的。最简单说,现在夏天到了,如果开了空调,我们可以把房间里的热量,通过空调传递给外面的空间。夏天外面的气温一般都是三十几度,当然我们空调的房间的设定都是二十几度。这时候,我们通过空调实现了把热从低温往高温传递这么一个过程。但是这里面,它会涉及到空调的介入,要耗电,对整个体系是有影响的,而不是没影响的。
所以热力学第二定律的克劳修斯表述,他说的是一定要不引起任何其他影响的这种过程是不可能的。但是这里还有一层意思,热如果只是从高温往低温移动,不引起其他任何影响的过程是可能的,但是反过来是不可能的。这里面有很深刻的物理内涵。从物理学上来说,我们破坏了高温跟低温这两端的对称性。就像我们说水为什么要从高处往低处流,我们都学过力学对吧,我们知道因为重力的存在,所以它要喜欢势能低的低处,所以高处跟低处是不对称的。但是我们现实生活里,这个不对称并不是显而易见的 ,对称性其实很多时候是广泛存在的。最简单比如说,在操场上有一个跑道,假设这跑道是东西走向的,跑道起点是在东边,或者设在西边,实际上是没有任何区别的,东边西边是对称的。
克劳修斯的整个热力学第二定律,它实际上就说了方向性问题,而且说高温跟低温是不一样的。所以这是一个非常深刻的物理学上的概念。这个表述是克劳修斯在1850年提出来的。
然后开尔文,前面杨老师介绍过,他也是整个热力学领域里一个奠基性的人物。他同样去看了卡诺定理的表述,然后他提出来另外一个概念,跟克劳修斯的说法,稍不一样的表述——不可能存在一种热机,从单一热源吸收热量全部转化为功,而不引起任何其他影响。所以这里面同样重要的,有一个界定,就是说:不产生任何其他影响。这里说的是,从单一热源吸收热量,全部转化为功是不可能的。回到刚才卡诺热机模型,它经历了一个循环之后,从一个高温过程吸热 ,然后绝热膨胀,然后再在低温放热,再绝热压缩回去,这个循环的初态跟终态是一样的,所以它是没有引起任何变化的。而且在整个循环过程中,它是对外做了功。这似乎和开尔文表述矛盾了?这里面涉及到两个热源,从高温热源吸热,然后到低温热源放热,而开尔文说的是,从单一热源吸热,然后再全部转变为功是不可能的。
如果我们回到刚才说的卡诺热机的效率问题,卡诺热机效率取决于高温热源跟低温热源的温度,跟工作介质无关。从单一的高温热源吸热然后转变为功,那就意味着这个热机的效率是百分之百。所以实际上开尔文的表述也就是说效率为百分之百的热机是不存在的。我们刚才说克劳修斯的整个表述,它是破坏了高温跟低温的一种对称性;开尔文的表述实际上它是破坏了功跟热的一种对称性。
我们前面已经听杨老师介绍过,功跟热是可以互相转换的,但是它不完全对称。我们通过做功,比如说摩擦做功 ,功是能非常好地转化为热,但是反过来不行,热不能百分之百地转化为功。所以功跟热,是可以相互转化 ,但是不是一个完全对称的过程。
下面我们简单看一下,这两种表述,我们为什么说它们是对等的。我们可以假设开尔文表述,里面说的过程是可能的,就是说有一个开尔文热机,能从一个单一的热源吸热,然后把它转化为功。这里产生的功还能拿过来当做空调用——把这个房间里的热量传输到外面去,这是另一个热机。当你把这两个热机合起来看时,开尔文表述的热跟功的完全转化,然后再联立一个空调的过程,先把热传到室外,然后室外再有一部分相同于刚才那部分功的热量,从室外传递给了开尔文热机的热源。所以它净的效果,就变成了从房间里有一部分热量,传到房间外,开尔文热机的热源也没有消耗热量,也没有出现一个净的功的输入或输出,所以你这么一联立就发现,如果开尔文说的事情不可能 ,那必然克劳修斯的表述也是不可能的。
通过设计这么一个过程,我们就简单地把两个表述对等起来,虽然表面上看,说的是两个不同的事情,一个是说高温跟低温的不对称性,也就是说低温到高温的传热而不引起变化是不可能的;另一个是说的,热跟功的一个不对称性,从单一热源吸收热量全部转化为功而不引起其他变化是不可能的。所以这两个表述表面上的不一致,实际上它背后对应的,是一样的概念。
我们甚至可以进一步推广,实际上热力学第二定律,除了这两种描述以外,更深刻更广泛地说,它说的就是,自然界里一切涉及热现象的宏观过程 ,都是不可逆的。这里面出现了一个新的概念,什么叫不可逆,我们在说不可逆之前,先得界定一下,什么叫做可逆。实际上我们在讲可逆之前,又涉及到,另外一个概念叫做平衡态。平衡态就是说把一个体系放在那放很久 ,它不发生任何变化,从宏观上来说,至少是我们看不到任何变化,那就是说我们这个体系处于平衡态。然后我们要定义可逆过程,一个过程,它跟平衡态是矛盾的,平衡态我们说的是不变化,一直不变,但过程是要说,从一个态变化到另一个态,怎么样能把这个过程把它串起来,实际上一个过程连接的是两个状态,我们可以把这两个状态中间,细分成很多很多个状态,这样从一个状态到下一个状态之间的变化是很小很小,这么一个很小的变化过程,叫做准静态过程。假设一个过程是,由一连串的准静态过程串起来的话,我们就把这个过程,叫做一个可逆过程。
可逆过程,它是一个实际过程的抽象,在我们实际过程里,是不存在一个可逆过程的,这是我们为了发展理论的描述抽象出来的一个概念。我们最开始介绍了整个卡诺热机的概念,我们提到了,里面有四个过程,一个是高温的吸热膨胀,再绝热膨胀,再到低温的吸热压缩、绝热压缩。这四个过程实际上都要求它是一个可逆的过程。由四个可逆的过程组成的卡诺循环代表的热机,效率最高 ,这就是最开始卡诺定理说的。卡诺定理跟我们前面说的克劳修斯表述、开尔文表述都是等价的。
开尔文跟克劳修斯,也是从引入热力学第一定律之后,回头看,发现要让卡诺定理成立,我们必须得再引入,两种描述中的其中一种,然后从那两种中,任何其中一种出发,我们能非常容易地来证明,卡诺的表述是成立的,熵的提出,考虑到实际过程都是不可逆的,克劳修斯把卡诺的这四个过程,做了一个推广,把可逆跟不可逆串起来的过程,然后再去探讨整个过程的吸热放热跟温度之间的关系。从这里,克劳修斯就引入了熵的概念。熵在这里实际上定义就是在某一个微小的过程中,假设温度不变,在一个恒温下,它从外界有一个吸收的热量,或者说放出的热量,而熵就是热量的变化对温度的一个比值。
熵也叫entropy,entropy是来源于希腊语。中文的熵,我们可以看到它是一个火字旁,表示它是跟热相关的,然后“商”代表的,是热量的变化跟温度的比值,所以我们中文熵这个字用得很好。现在熵经常用一个符号来替代用S。为什么大家习惯性地用S呢?这是为了纪念大物理学家卡诺。卡诺的名字里,有一个是S开头的,所以我们熵是一直用S来代表。
引入熵之后,假设我们考虑的是一个闭合孤立的体系。那我们就可以发现,孤立的系统的一个实际过程,熵都是在增加的。在这个阶段,我们说系统熵一直在增加,等于只是说,过程不可逆的。在我们热力学里,熵它实际上是第二位的,就是说,温度是第一位的,它是可测量的,熵这里还没有,自己独立的定义。
熵与微观过程,到了玻尔兹曼那儿联系了起来。我们再去看热力学第二定律,看热力学第一定律,然后把它结合起来,通过对比,我们就能发现,熵这时候会得到一个独立的含义。熵这时候就代表了整个体系里面包含的状态数。所以这时候熵增就是说,可能有的微观状态在变多,也就是系统从一个更有序,变成了一个更无序的状态。我们如果把整个宇宙,看做一个孤立体系,整个宇宙里的过程,也是对应一个熵增的过程,所以这也是为什么,有时候我们把熵的增加,叫做时间箭头的原因。
这里再最后再补充一点的是什么呢,一个宏观过程,它为什么是不可逆的?我们大家都学过力学,力学上整个过程是可逆的。因为我们看的是一个比较小的体系,一个物体我施加一个力,它是怎么运动,然后如果反过来,时间反着走,那它应该是回到初始的状态 ,所以这叫可逆。那我现在假设真实的一个宏观体系,一堆气体它也是由一个个粒子组成的,我们不管它是遵循经典力学也好,遵循一个量子力学的描述也好,按道理它应该都是可逆的。所以这儿问题就出来了。在经典力学跟量子力学层面上来讲的话过程都是可逆的,为什么到了热力学这里,过程就变成了不可逆?
这个是困扰了玻尔兹曼很长很长时间的问题,这里面是有涉及到两个层次的概念。因为我们在测量信息的时候,是在宏观层次上测量,我们刚才说要把经典力学或者说量子力学,应用到一个个粒子的时候,那是在微观层次上的一个问题,一个宏观的体系,通常包含很多很多的微观粒子 ,10的23次方,这是很大的一个数字。从经典力学跟量子力学的可逆性,到热力学的不可逆性,它实际上涉及到在不同层次跨越的时候信息丢失。当然这里只是给大家一个初步的印象,严格的数学证明,是一个非常深奥的问题,我们有机会再跟大家细细讲解。
本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。