 解题过程:
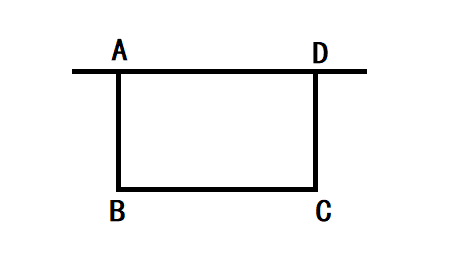
根据矩形的性质和题目中的条件:四边形ABCD为矩形,则AD=BC,AB=CD,∠BAD=∠ADC=∠B=∠C=90°;
解题过程:
根据矩形的性质和题目中的条件:四边形ABCD为矩形,则AD=BC,AB=CD,∠BAD=∠ADC=∠B=∠C=90°;
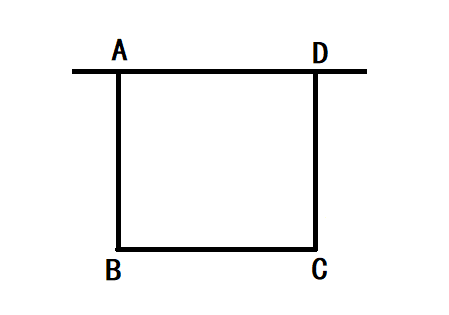 1、AD=AB
根据题目中的条件和结论:AD=BC,AB=CD,AD=AB,则AB=BC=CD=AD;
当PB=BC时
根据结论:AB=BC,PB=BC,则点P与点A重合;
当PC=BC时
根据结论:BC=CD,PC=BC,则点P与点D重合;
当PB=PC时
1、AD=AB
根据题目中的条件和结论:AD=BC,AB=CD,AD=AB,则AB=BC=CD=AD;
当PB=BC时
根据结论:AB=BC,PB=BC,则点P与点A重合;
当PC=BC时
根据结论:BC=CD,PC=BC,则点P与点D重合;
当PB=PC时
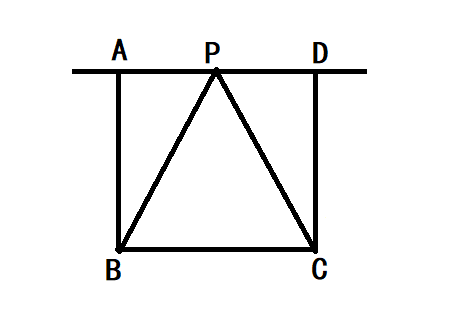 根据全等三角形的判定:∠BAD=∠ADC=90°,AB=CD,PB=PC,则Rt△PAB≌Rt△PDC;
根据全等三角形的性质和结论:Rt△PAB≌Rt△PDC,则PA=PD,即点P是AD的中点;
所以,当AB=AD=4时,满足△PBC是等腰三角形点P有且只有3个。
2、AD<AB
根据结论:AD<AB,PB≥AB,PC≥AB,则PB>AD,PC>AD;
根据结论:AD=BC,PB>AD,PC>AD,则PB>BC,PC>BC,即不存在满足PB=BC或PC=BC的等腰三角形△PBC;
根据全等三角形的判定:∠BAD=∠ADC=90°,AB=CD,PB=PC,则Rt△PAB≌Rt△PDC;
根据全等三角形的性质和结论:Rt△PAB≌Rt△PDC,则PA=PD,即点P是AD的中点;
所以,当AB=AD=4时,满足△PBC是等腰三角形点P有且只有3个。
2、AD<AB
根据结论:AD<AB,PB≥AB,PC≥AB,则PB>AD,PC>AD;
根据结论:AD=BC,PB>AD,PC>AD,则PB>BC,PC>BC,即不存在满足PB=BC或PC=BC的等腰三角形△PBC;
 当PB=PC时,点P是AD的中点;
所以,当AD<AB时,满足△PBC是等腰三角形点P有且只有1个,不符合条件。
3、AD>AB
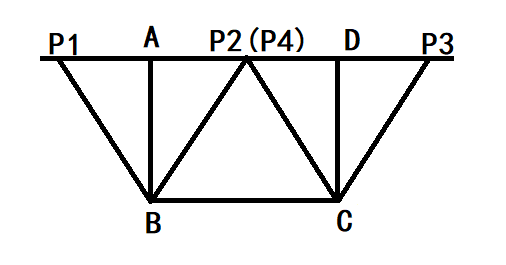
PB=BC时存在两种情况点P1、P2,PC=BC上存在两种情况点P3、P4,当P2与P4重合时,P2B=BC=P4C,此时满足△PBC是等腰三角形点P有且只有3个;
根据结论:P2B=BC=P4C,则△PBC是等边三角形;
根据等边三角形的性质和结论:△PBC是等边三角形,则∠P2BC=60°;
根据结论:∠ABC=90°,∠P2BC=60°,则∠ABP2=30°;
根据直角三角形的性质和结论:∠BAD=90°,∠ABP2=30°,则BP2=2AP2;
根据结论:点P是AD的中点,AD=4,则AP2=2;
根据结论:BP2=2AP2,AP2=2,则BP2=4;
根据勾股定理和结论:∠BAD=90°,AP2=2,BP2=4,则AB=2√3;
所以,当AB=2√3时,满足△PBC是等腰三角形点P有且只有3个。
综上,当AB=4或2√3时,满足△PBC是等腰三角形点P有且只有3个。
结语
解决本题的关键是根据矩形两组边长之间的数量关系,判断满足等腰三角形条件的不同情况下的线段长度。
当PB=PC时,点P是AD的中点;
所以,当AD<AB时,满足△PBC是等腰三角形点P有且只有1个,不符合条件。
3、AD>AB
PB=BC时存在两种情况点P1、P2,PC=BC上存在两种情况点P3、P4,当P2与P4重合时,P2B=BC=P4C,此时满足△PBC是等腰三角形点P有且只有3个;
根据结论:P2B=BC=P4C,则△PBC是等边三角形;
根据等边三角形的性质和结论:△PBC是等边三角形,则∠P2BC=60°;
根据结论:∠ABC=90°,∠P2BC=60°,则∠ABP2=30°;
根据直角三角形的性质和结论:∠BAD=90°,∠ABP2=30°,则BP2=2AP2;
根据结论:点P是AD的中点,AD=4,则AP2=2;
根据结论:BP2=2AP2,AP2=2,则BP2=4;
根据勾股定理和结论:∠BAD=90°,AP2=2,BP2=4,则AB=2√3;
所以,当AB=2√3时,满足△PBC是等腰三角形点P有且只有3个。
综上,当AB=4或2√3时,满足△PBC是等腰三角形点P有且只有3个。
结语
解决本题的关键是根据矩形两组边长之间的数量关系,判断满足等腰三角形条件的不同情况下的线段长度。 本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。







