一,高斯公式应用的举例
首先举两个简单的高斯公式应用的例子。
例一:
有一个长方体的游泳池,处于满水状态。泳池底部有一个加水孔。疯狂泳池管理员打开了加水开关,此时水会从泳池的顶部向外哗哗溢出来。
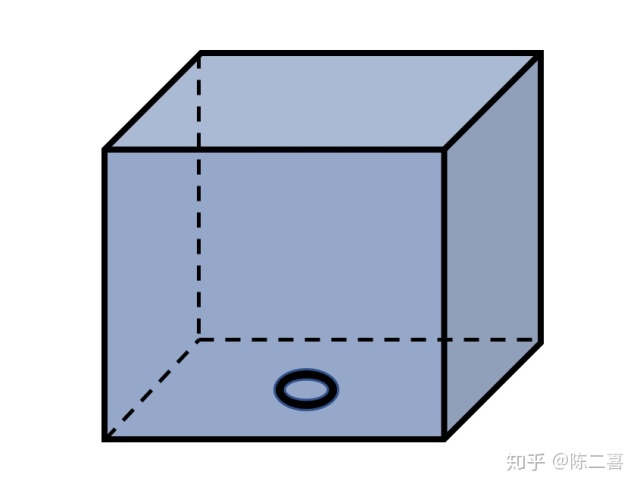
充满水的泳池,底部为加水孔 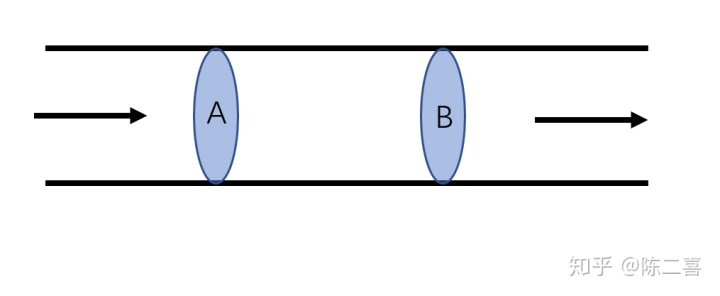
管道中选取A、B两个截面 ![[公式]](https://www.zhihu.com/equation?tex=%5COmega) ,这个区域内充满了水。围成这块区域的边界为
,这个区域内充满了水。围成这块区域的边界为 ![[公式]](https://www.zhihu.com/equation?tex=%5CSigma) (泳池的底、和四面墙以及顶部构成了边界
(泳池的底、和四面墙以及顶部构成了边界 ![[公式]](https://www.zhihu.com/equation?tex=%5CSigma) ),那么我们可以得出:
),那么我们可以得出:
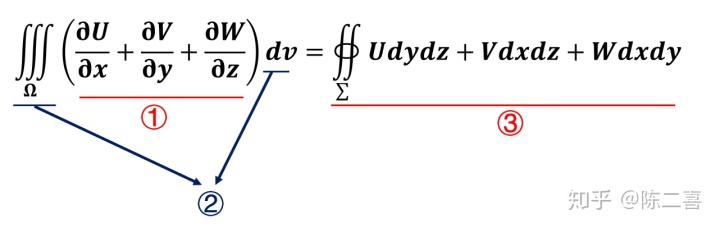
![[公式]](https://www.zhihu.com/equation?tex=%5COmega) ,即整个游泳池,表示的意义就是把泳池中无数个无限小的区域向外释放的水的体积给全部加起来。
综上,等号左边表示的意义就是:泳池内部总的进水量。
第三部分是一个封闭曲面积分,对象为
,即整个游泳池,表示的意义就是把泳池中无数个无限小的区域向外释放的水的体积给全部加起来。
综上,等号左边表示的意义就是:泳池内部总的进水量。
第三部分是一个封闭曲面积分,对象为 ![[公式]](https://www.zhihu.com/equation?tex=%5CSigma) ,即泳池的六个边界。表示的物理意义是,泳池通过边界向外泄露的水量。
所以,高斯公式就是在表达,泳池通过进水口的进水体积,等于通过泳池边界排出去的水的体积。
从这个角度来看,高斯公式很容易理解。
=============
三,物理意义很简单,但为什么要这么写。
下面解释一下,上文中,高斯公式的三部分为什么那么写。
1, 先从等号右边说起。
等号右边所代表的物理意义叫通量。通量是一个物理学上的概念,是强度与(有效)面积的乘积。
比如,高中所学的磁通量
,即泳池的六个边界。表示的物理意义是,泳池通过边界向外泄露的水量。
所以,高斯公式就是在表达,泳池通过进水口的进水体积,等于通过泳池边界排出去的水的体积。
从这个角度来看,高斯公式很容易理解。
=============
三,物理意义很简单,但为什么要这么写。
下面解释一下,上文中,高斯公式的三部分为什么那么写。
1, 先从等号右边说起。
等号右边所代表的物理意义叫通量。通量是一个物理学上的概念,是强度与(有效)面积的乘积。
比如,高中所学的磁通量 ![[公式]](https://www.zhihu.com/equation?tex=%5CPhi%3DB%5Cbullet+S) ,B就是磁感应强度,S表示正对面积。
在日常生活以及流体力学中,我们通常把通量叫做流量。单位为L/S,也就是单位时间内流过的体积。
现在的问题是,如何计算水穿过复杂的边界
,B就是磁感应强度,S表示正对面积。
在日常生活以及流体力学中,我们通常把通量叫做流量。单位为L/S,也就是单位时间内流过的体积。
现在的问题是,如何计算水穿过复杂的边界 ![[公式]](https://www.zhihu.com/equation?tex=%5CSigma) 流出去的体积。
先考虑简单的一维情况:
流出去的体积。
先考虑简单的一维情况:
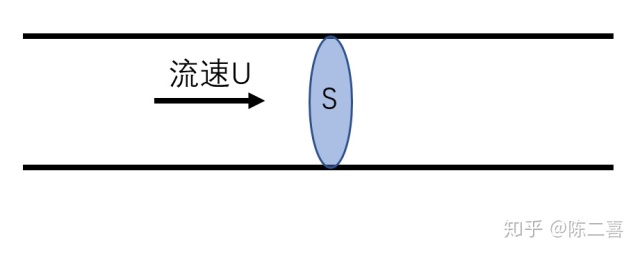
![[公式]](https://www.zhihu.com/equation?tex=U%5Cbullet+S) ,写成微分形式为
,写成微分形式为 ![[公式]](https://www.zhihu.com/equation?tex=UdS) ,其中,S表示正对的有效面积,也就是说,S与D垂直。
一维情况很容易理解。
如果考虑真实的三维情况,我们需要借助向量这个有利工具。
在三维情况下,水的流速并不是只朝着一个方向,而是沿着x,y,z三个方向上都有分量,这三个分量可以设为U,V,W。
上段说到,截面积为与速度垂直的有效面积,既然速度有三个方向的分量,那么速度垂直穿过的面积就有三个方向,分别为yz平面,xz平面, xy平面。
,其中,S表示正对的有效面积,也就是说,S与D垂直。
一维情况很容易理解。
如果考虑真实的三维情况,我们需要借助向量这个有利工具。
在三维情况下,水的流速并不是只朝着一个方向,而是沿着x,y,z三个方向上都有分量,这三个分量可以设为U,V,W。
上段说到,截面积为与速度垂直的有效面积,既然速度有三个方向的分量,那么速度垂直穿过的面积就有三个方向,分别为yz平面,xz平面, xy平面。
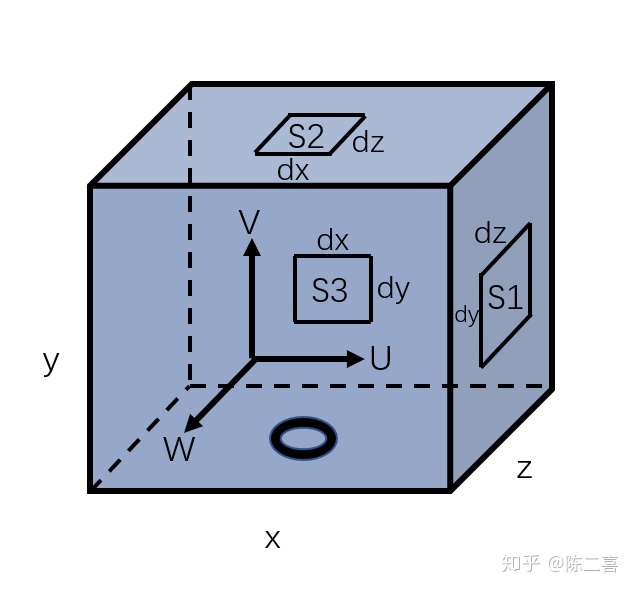
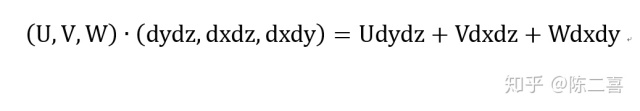
![[公式]](https://www.zhihu.com/equation?tex=%5CSigma) 的总流量:
的总流量:
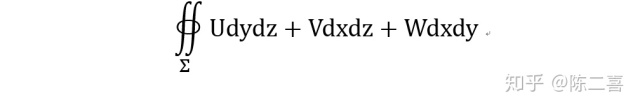
![[公式]](https://www.zhihu.com/equation?tex=%5CDelta+x%2C%5CDelta+y%2C%5CDelta+z) ,三者相等。为了简化作图,我只考虑x轴方向上的一条边AB,经过时间
,三者相等。为了简化作图,我只考虑x轴方向上的一条边AB,经过时间 ![[公式]](https://www.zhihu.com/equation?tex=%5CDelta+t) 变为A’B’。
变为A’B’。

![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%5Cpartial+U%7D%7B%5Cpartial+x%7D) 上述变化率再乘以AB的原长
上述变化率再乘以AB的原长 ![[公式]](https://www.zhihu.com/equation?tex=%5CDelta+x) ,便可得到B相对于A的速度:
,便可得到B相对于A的速度: ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%5Cpartial+U%7D%7B%5Cpartial+x%7D%5CDelta+x) 上述速度乘以时间
上述速度乘以时间 ![[公式]](https://www.zhihu.com/equation?tex=%5CDelta+t) ,便得到B相对于A的位移:
,便得到B相对于A的位移: ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%5Cpartial+U%7D%7B%5Cpartial+x%7D%5CDelta+x+%5CDelta+t) 上述位移加上原长
上述位移加上原长 ![[公式]](https://www.zhihu.com/equation?tex=%5CDelta+x) ,便得到新的微团的长度:
,便得到新的微团的长度: ![[公式]](https://www.zhihu.com/equation?tex=%5CDelta+x%2B%5Cfrac%7B%5Cpartial+U%7D%7B%5Cpartial+x%7D%5CDelta+x+%5CDelta+t) 同理,新的微团的宽度为:
同理,新的微团的宽度为: ![[公式]](https://www.zhihu.com/equation?tex=%5CDelta+y%2B%5Cfrac%7B%5Cpartial+V%7D%7B%5Cpartial+y%7D%5CDelta+y+%5CDelta+t) 新的微团的厚度为:
新的微团的厚度为: ![[公式]](https://www.zhihu.com/equation?tex=%5CDelta+z%2B%5Cfrac%7B%5Cpartial+W%7D%7B%5Cpartial+z%7D%5CDelta+z+%5CDelta+t) 所以,新微团的体积变为
所以,新微团的体积变为
![[公式]](https://www.zhihu.com/equation?tex=%28%5CDelta+x%2B%5Cfrac%7B%5Cpartial+U%7D%7B%5Cpartial+x%7D%5CDelta+x+%5CDelta+t%29%28%5CDelta+y%2B%5Cfrac%7B%5Cpartial+V%7D%7B%5Cpartial+y%7D%5CDelta+y+%5CDelta+t%29%28%5CDelta+z%2B%5Cfrac%7B%5Cpartial+W%7D%7B%5Cpartial+z%7D%5CDelta+z+%5CDelta+t%29) 减去原微团的体积,得到相对体积变化量:
减去原微团的体积,得到相对体积变化量:
![[公式]](https://www.zhihu.com/equation?tex=%28%5CDelta+x%2B%5Cfrac%7B%5Cpartial+U%7D%7B%5Cpartial+x%7D%5CDelta+x+%5CDelta+t%29%28%5CDelta+y%2B%5Cfrac%7B%5Cpartial+V%7D%7B%5Cpartial+y%7D%5CDelta+y+%5CDelta+t%29%28%5CDelta+z%2B%5Cfrac%7B%5Cpartial+W%7D%7B%5Cpartial+z%7D%5CDelta+z+%5CDelta+t%29-%5CDelta+x%5CDelta+y%5CDelta+z) 上述相对体积变化量除以原微团体积,得到相对体积变化率:
上述相对体积变化量除以原微团体积,得到相对体积变化率:
![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%28%5CDelta+x%2B%5Cfrac%7B%5Cpartial+U%7D%7B%5Cpartial+x%7D%5CDelta+x+%5CDelta+t%29%28%5CDelta+y%2B%5Cfrac%7B%5Cpartial+V%7D%7B%5Cpartial+y%7D%5CDelta+y+%5CDelta+t%29%28%5CDelta+z%2B%5Cfrac%7B%5Cpartial+W%7D%7B%5Cpartial+z%7D%5CDelta+z+%5CDelta+t%29-%5CDelta+x%5CDelta+y%5CDelta+z%7D%7B%5CDelta+x%5CDelta+y%5CDelta+z%7D) 这个变化率还要除以时间
这个变化率还要除以时间 ![[公式]](https://www.zhihu.com/equation?tex=%5CDelta+t) ,便得到单位时间内的相对体积变化率:
,便得到单位时间内的相对体积变化率:
![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%28%5CDelta+x%2B%5Cfrac%7B%5Cpartial+U%7D%7B%5Cpartial+x%7D%5CDelta+x+%5CDelta+t%29%28%5CDelta+y%2B%5Cfrac%7B%5Cpartial+V%7D%7B%5Cpartial+y%7D%5CDelta+y+%5CDelta+t%29%28%5CDelta+z%2B%5Cfrac%7B%5Cpartial+W%7D%7B%5Cpartial+z%7D%5CDelta+z+%5CDelta+t%29-%5CDelta+x%5CDelta+y%5CDelta+z%7D%7B%5CDelta+x%5CDelta+y%5CDelta+z%5CDelta+t%7D) 上述结果化简后便得到
上述结果化简后便得到 ![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%5Cpartial+U%7D%7B%5Cpartial+x%7D%2B%5Cfrac%7B%5Cpartial+V%7D%7B%5Cpartial+y%7D%2B%5Cfrac%7B%5Cpartial+W%7D%7B%5Cpartial+z%7D) 所以,对于每一个无限小的微团,单位时间内,其体积的相对变化为:
所以,对于每一个无限小的微团,单位时间内,其体积的相对变化为:
![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%5Cpartial+U%7D%7B%5Cpartial+x%7D%2B%5Cfrac%7B%5Cpartial+V%7D%7B%5Cpartial+y%7D%2B%5Cfrac%7B%5Cpartial+W%7D%7B%5Cpartial+z%7D) 对上述结果进行体积分,便得到单位时间内整个泳池内部所有微团产生的体积之和,
即为高斯公式左边部分。
上述是高斯公式左半部分的详细推导过程,看看即可,并不要求推导。
因为,有一个现成的概念:散度
================
微积分课程上提到过三个类似的概念,分别为梯度、散度、旋度。这三个概念中都含有哈密顿算子
对上述结果进行体积分,便得到单位时间内整个泳池内部所有微团产生的体积之和,
即为高斯公式左边部分。
上述是高斯公式左半部分的详细推导过程,看看即可,并不要求推导。
因为,有一个现成的概念:散度
================
微积分课程上提到过三个类似的概念,分别为梯度、散度、旋度。这三个概念中都含有哈密顿算子 ![[公式]](https://www.zhihu.com/equation?tex=%5Cbigtriangledown%3D%28%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+x%7D%2C%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+y%7D%2C%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+z%7D%29) ,是一个矢量。
对一个向量(u,v,w),取散度,应该为
,是一个矢量。
对一个向量(u,v,w),取散度,应该为 ![[公式]](https://www.zhihu.com/equation?tex=%28%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+x%7D%2C%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+y%7D%2C%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+z%7D%29%5Cbullet+%28U%2CV%2CW%29) ,
两个向量点乘,应该得一标量,上式结果为:
,
两个向量点乘,应该得一标量,上式结果为:
![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%5Cpartial+U%7D%7B%5Cpartial+x%7D%2B%5Cfrac%7B%5Cpartial+V%7D%7B%5Cpartial+y%7D%2B%5Cfrac%7B%5Cpartial+W%7D%7B%5Cpartial+z%7D) 这坨东西就叫做散度。
散度所表达的意思就是:对一个无限小的微团,内部通过微团的边界向外界释放、流出的流量。
这就是散度的最基本的定义。
对上述散度求体积分,便得到高斯公式等号左边的内容。
综上:高斯公式等号左边表达的意思就是:把泳池分成无数多个无限小的区域。把每个区域向外释放的水的体积加起来,得到的总量,就是通过进水口向泳池进水的体积。
结合本节1,2两部分,可以知道,高斯公式在阐述:
通过泳池的进水口流进泳池的水,等于通过泳池边界漏出去的水。
==============
这看似是一句废话。但是
从数学角度上来说,高斯公式建立了体积分与面积分之间的联系。
从物理角度上来说,高斯公式建立了整体与边界之间的联系。
从哲学角度上来说,高斯公式告诉我们,内部变化一定可以通过表面变化看出来。
这坨东西就叫做散度。
散度所表达的意思就是:对一个无限小的微团,内部通过微团的边界向外界释放、流出的流量。
这就是散度的最基本的定义。
对上述散度求体积分,便得到高斯公式等号左边的内容。
综上:高斯公式等号左边表达的意思就是:把泳池分成无数多个无限小的区域。把每个区域向外释放的水的体积加起来,得到的总量,就是通过进水口向泳池进水的体积。
结合本节1,2两部分,可以知道,高斯公式在阐述:
通过泳池的进水口流进泳池的水,等于通过泳池边界漏出去的水。
==============
这看似是一句废话。但是
从数学角度上来说,高斯公式建立了体积分与面积分之间的联系。
从物理角度上来说,高斯公式建立了整体与边界之间的联系。
从哲学角度上来说,高斯公式告诉我们,内部变化一定可以通过表面变化看出来。


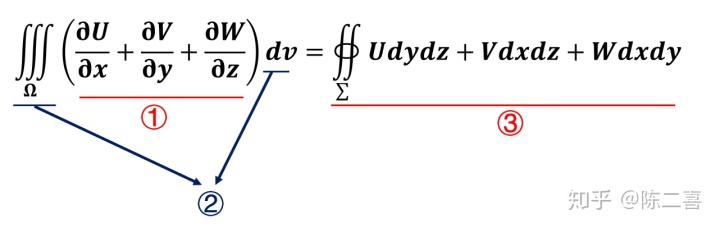


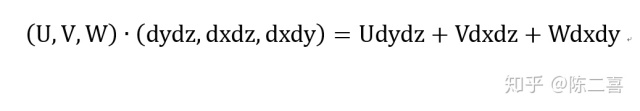
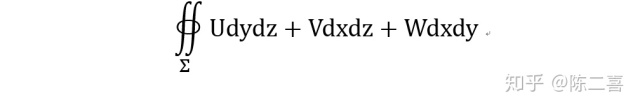

本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。