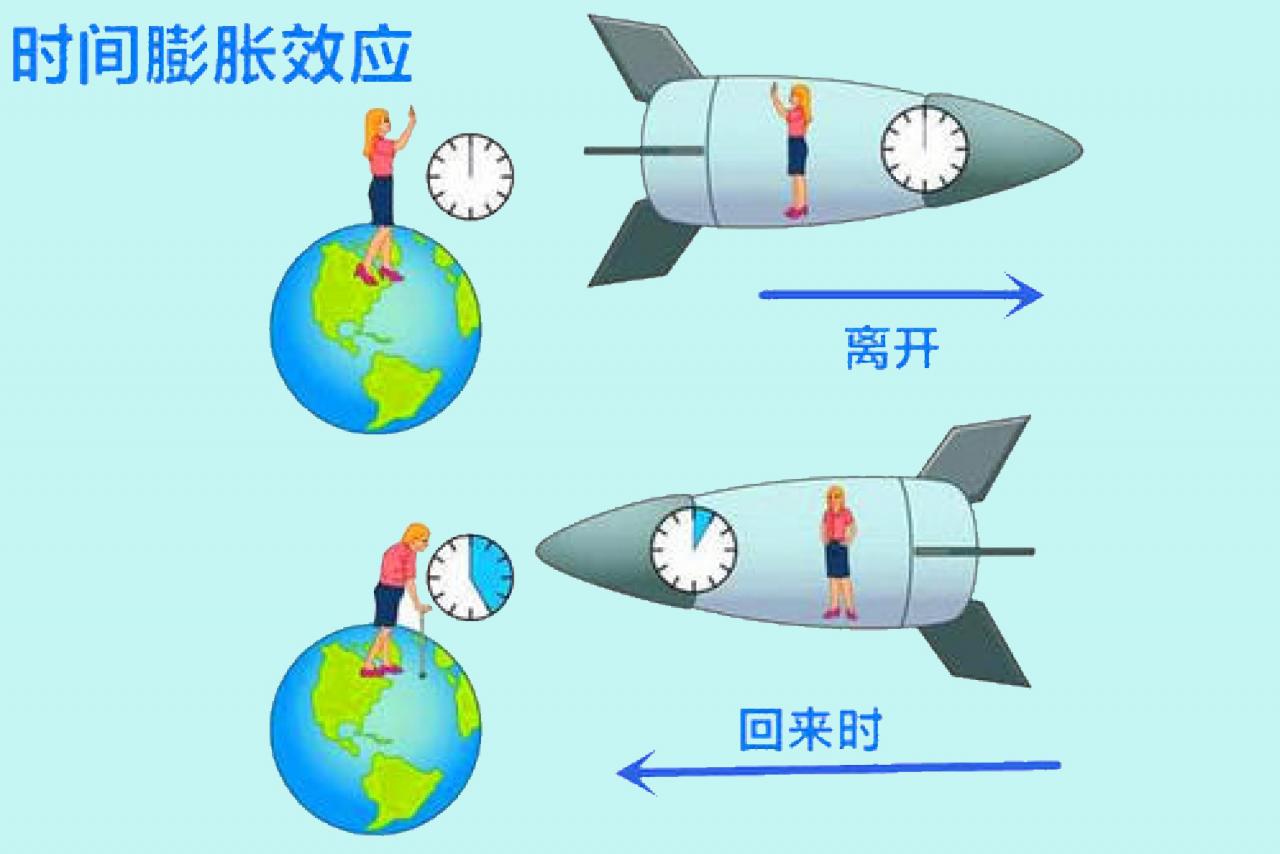
时空弯曲理论和时间膨胀理论都是爱因斯坦相对论的内容。在狭义相对论中,爱因斯坦主要阐明了速度和时间的关系,一般叫做速度时间膨胀问题;而在广义相对论中,着重说明时间与空间弯曲的关系,也就是引力时间膨胀的问题。
爱因斯坦相对论的核心内容就是阐述时间、空间和物质三者关系的,通过一系列详实的数理逻辑论证,认为时间、空间、物质是三位一体的,论证了在不同坐标系中,时空具有相对性,这从根本上颠覆了经典物理学的绝对时空观。
论证过程很复杂,这里就不说了。结论很简单,就是在不同速度和不同引力场中,时间会膨胀,通俗明白点说,就是速度越快的坐标系中,会有尺缩钟慢效应,距离会缩得越缩短,时间流逝会越慢;而在引力越大的坐标系里,时间就会流逝得越慢。
但有两个天花板:光速和黑洞史瓦西半径里面,是时间和空间的终点。当物体运动达到光速时,或者进入时空曲率无限大(引力无限大)的黑洞视界以内时,空间为零,时间将停止。
但光速使我们世界的天花板,凡有静止质量的物体都无法达到,更无法突破,这是因为质增效应。当物体趋于接近光速时,其动能和质量将会变得无限大。这就是说,即便是1个基本粒子,如果要达到光速,其所需能量和达到的动量也将无限大。
而我们宇宙也是有限的,也就是说,不可能有无限的能量来推动一个有静止质量的物体达到光速,而达到光速这个粒子的动量将超过宇宙质量,这本来就是个悖论。这个问题我过去已经解释过多次,今天就不展开说了。
现在我们只通过两个时间膨胀公式,来说说时间与速度和空间的关系。
狭义相对论给出的速度时间膨胀公式为:t'=t/√[1-(v/c)?]
式中,t'是速度时间膨胀效应值;t是低速系观测者第一个时钟时间记录;v是第二个时钟相对第一个时钟的移动速度;c为光速。
广义相对论给出的引力时间膨胀计算公式为:t'=tx√(1-2GM/rc?)
式中,t'为引力时间膨胀效应值;t为低引力惯性系观测者时间流逝值;G为引力常数,取值6.67x10^-11N·m?/kg?;M为天体质量;r为天体半径;c为光速。
期间的推导过程很复杂,就留给那些质疑相对论的“高手”们去挑刺用吧,我们科普就没必要了解那么高深了。
根据速度时间膨胀效应公式计算,当一个物体运动速度达到光速的一半,也就是每秒约15万千米时,时间膨胀会达到1.15倍,也就是会慢15%,这样飞船里的人过了1年,地球人就过了1.15年。
而达到光速的99%时,时间膨胀效应会达到7倍,也就是飞船里的人过了1年,地球上的人过去了7年;而光速达到99.999999999999%时,时间会膨胀707万倍,飞船的人过了1年,地球人就过了707万年。
同样,在引力越大的坐标系,时间膨胀得越厉害,也就是时间流逝越慢。在《星际穿越》这部科幻影片中,飞船到达一个在黑洞附近的米勒星球,这颗黑洞是太阳质量的1亿倍,电影没有给出距离黑洞视界多远的距离,但给出宇航员们在那里呆1小时,地球就过去了7年,也就是时间膨胀了6万多倍。
因此当宇航员库珀回到地球时,他还是老样子,而其女儿已经90多岁了。
宇宙中已知最大黑洞SDSS J073739.96 384413.2的质量是太阳的1040亿倍,在其附近时间膨胀会有多少呢?给出距离黑洞视界的距离,我们就可以根据公式计算出来。
许多人根本不屑于学习相对论的相关知识,凭着吃喝拉撒的逻辑就否定时间膨胀理论,但不管这些人相信不相信,时间膨胀理论早就应用在科学研究和各种技术应用中。最典型和常用的例子就是导航定位系统,如果没有对卫星和地面时间做出相对论调校,导航就会把你导到爪哇国去了。
我的回答是NO。
许多网友都有一个误区:既然在高速飞船或者大引力场附近,时间流逝变慢,那么在这种坐标系里面生活的人不就长寿了?
其实完全不是这回事。因为在这种坐标系里的人们,感受到的时间还是正常流逝的,一点也没有变慢。时间1分1秒,1小时1天的感觉与地球上是一样的。如果我们忽略太空旅行的各种影响因素,比如辐射、失重等等,他们的寿命是没有任何变化的。
也就是说他们在地球上能活100岁,在飞船里还是只能活100岁。
而实际上,太空旅行的条件远远不如地球这么安全,因此在同等医疗保障条件下,还会大大影响寿命呢。但他们如果回到地球,与地球人的时间流逝来比,则会发现地球人流逝的时间比他们快。快多少,就要看他们飞船的速度有多快,或他们呆的引力场有多大,时间有多长了。
根据速度时间膨胀公式计算,如果乘坐99.99%光速的飞船,飞了1年回来,地球人就过去了70年;如果乘坐99.999999999999%光速的飞船,到254万光年的仙女座星系回来,旅行者们只用了0.7年,也就是8个多月时间,而地球已经过去了508万年。
如果乘坐的飞船很慢,在光速的50%以下,甚至更慢,时间膨胀效应就很小了,影响也就不大了。而现在的飞船速度还只有每秒十几千米,旅行者时间膨胀效应相对地球生活的人来说,就完全可以忽略不计了。
时间膨胀效应并不是感觉时间变慢了,而是根本没感觉。所谓尺缩钟慢效应,可以理解为速度越快,距离就越缩短了,时间就不需要那么多了。缩短了多少呢?这与时间膨胀的倍数是对应的。
比如乘坐99.999999999999%光速的飞船前往254万光年距离的仙女座星系,时间膨胀了707万倍,这样就等于距离缩短了707万倍,因此254万光年的路程就只有约0.35光年,来回路程就只有0.7光年了,飞船的速度接近光速,时间当然就只要约0.7年了。
这个计算只是为了说明这个问题的理论值,忽略了加速减速和停留的时间,请勿在此钻牛角尖。
因此,飞船上的人们不是感觉只过了这么久,而是实实在在只过了这么久。这种时间流逝速度不是表面的,而是骨子里的。从他们的意识感觉和身上每一个细胞,乃至组成细胞的各种原子元素,新陈代谢周期都只是经历了这个时间的变化。
在重力系统中的时间膨胀效应也是一样的。
因此,高速旅行者们只是相比在地球相对静止的人们,只是时间本身“流逝”得更慢而已,而对于他们自己来说,真正的感觉还是过了1天就是1天,没有感觉到多得到到1点时间。
这有点像我们常说的冻龄,也就是年龄冻住了,或者说把人们雪藏冰冻起来,过了许多年再让其苏醒过来,在苏醒的人们看来,世上已经过去很多年,但这能够说是冰冻的人长寿了吗?
时间膨胀效应是一种客观存在,是宇宙规律,带给宇宙航行的人们并没有什么好处,反而会增添许多困扰。比如真的有接近光速的飞船,离开地球前往某个星球的人们回来后,亲人们都离去了,地球已经是沧海桑田了,这种探索或者旅行有什么意义呢?
因此,未来的深空旅行,提升速度只是一个方面。当速度在光速的50以下时,时间膨胀效应困扰还不算太大,人们还是可以接受的。但更快的旅程,很可能就不是依靠速度提升了,而是另辟蹊径。
目前科学界认为有可能突破深空航行速度瓶颈的方法有两种,即虫洞穿越和曲速引擎。通俗地说,这两种方式就是采取钻隧道、抄近道的跨越方式到达目的地,从总体旅行的距离和时间来看,似乎超越光速多少倍,但实际上并没有提升速度,因此不受光速藩篱限制,也不会出现什么速度膨胀效应。
现在这些方式还处于科幻阶段,未来是否真的能够实现很难说。
时空通讯原创版权 本站内容收集整理于网络,多标有原文出处,本站仅提供信息存储空间服务。如若转载,请注明出处。